In matematica l’arte di porre problemi deve essere tenuta in maggiore considerazione di quella di risolverli.
(Georg Cantor)
Indice
La teoria degli insiemi
Ci si trova in genere in difficoltà a spiegare gli argomenti di teoria degli insiemi, seppur a prima vista semplici, ed un sintomo delle incertezze dominanti sta nella terminologia stessa, che talvolta si riferisce alla “teoria degli insiemi” e altre volte a una non ben specificata “insiemistica”, senza che ci sia chiarezza sulla differenza e sugli eventuali motivi della distinzione. Con “insiemistica” sembra si voglia alludere a un complesso di argomenti non governati da una teoria e senza un obiettivo caratterizzante, un dominio di conoscenze dai confini incerti, quasi non si trattasse di una teoria definita. Ma cosa si intende con “insiemistica”?
Nell’insiemistica rientrano in genere due temi: il primo riguarda le operazioni booleane di unione, intersezione e complemento, tra i sottoinsiemi di un universo fissato. Ma le proprietà di queste operazioni non sono altro che le proprietà dei connettivi logici, disgiunzione, congiunzione e negazione. Con questa osservazione non si vuole suggerire che oltre alla teoria degli insiemi si debba anche studiare la logica proposizionale delle tavole di verità –con le quali purtroppo si identifica la logica – ma semplicemente ricordare che basta saper parlare bene, con proprietà, per padroneggiare le particelle logiche e quindi le relazioni booleane tra insiemi. Sarebbe meglio dedicarsi alla cura della lingua.
Le difficoltà, se ci sono, sono difficoltà di rappresentazione: vedere insiemi sulla pluralità di oggetti che ci circondano. La new math è crollata sul singoletto, e giustamente: distinguere un oggetto x dall’insieme {x} il cui unico elemento è x è qualcosa che ha senso solo nel mondo dei concetti, non in quello dell’esperienza; è imposto da ragioni superiori, non è la base su cui poggiare quelle ragioni. Non parliamo della differenza tra l’insieme vuoto ∅ e {∅}, un insieme che non è vuoto ma che contiene solo il vuoto. Lo stesso ostacolo per i non matematici, e per i principianti, sta nel concepire o vedere l’insieme P(x) dei sottoinsiemi di un insieme x, che non esiste in natura neanche se x è concreto, e prima ancora due insiemi non disgiunti, che non si possono fisicamente isolare.
L’altro contenuto dell’insiemistica comprende la definizione di funzione, con i necessari preliminari, che iniziano dalle coppie ordinate, dal prodotto cartesiano e dalle relazioni. Quindi vengono le diverse definizioni relative alle funzioni, come immagine e controimmagine, restrizione, iniettività, suriettività ecc.
Ma questo è linguaggio, dove è la teoria? Inoltre è un linguaggio estremamente estrinseco e preliminare, come imparare a denotare vertici, spigoli e facce quando si parla di poliedri. Un livello matematico superiore nel quale interviene il linguaggio insiemistico è quello dell’algebra, intesa come teoria delle strutture. Anche in questo caso tuttavia la presenza del linguaggio insiemistico è ancillare; delle strutture interessano infatti le proprietà algebriche, o topologiche, matematiche insomma. Come se la teoria degli insiemi non fosse matematica. Questa idea si rafforza ab absentia, per la congiura del silenzio. Nella vulgata la teoria degli insiemi avrebbe un carattere elementare e propedeutico, e perciò stesso povero di applicazioni.
Il problema non riguarda solo l’insegnante, pure il matematico medio che fa ricerca si trova in stato di ignoranza rispetto al contenuto e al valore degli argomenti di teoria degli insiemi. Si può tranquillamente affermare, sulla base di molta esperienza, che i matematici non sanno cosa è la teoria degli insiemi.
D’altra parte la disciplina non è presente nei normali curricula e l’ignoranza è inevitabile, anzi programmata. La preparazione universitaria di chi fa ricerca non è molto diversa da quella degli insegnanti, a parte l’approfondimento degli argomenti verso i quali si orienta il lavoro di tesi nell’indirizzo scelto. La strutturazione attuale dei piani di studio perpetua la trasmissione di diverse lacune; nel caso della teoria degli insiemi questa circostanza dipende da una reale difficoltà, tecnica ma con intrecci politici, perché la teoria è una teoria un po’ speciale, e diversa dalle altre: non è possibile studiarla a fondo e padroneggiarla senza usare alcuni strumenti e concetti della logica matematica. La mancanza di una intuizione collaudata richiede che ci si appoggi in modo più sostanziale che per altri argomenti sulle definizioni e in generale sul linguaggio, che è la cosa più concreta a disposizione. Questo peraltro è uno degli aspetti interessanti del suo insegnamento, anche pre-universitario: l’opportunità di introdurre al pensiero astratto e alla capacità di formalizzazione. Si tratterebbe comunque di concetti molto elementari e, questi sì, propedeutici a tutta la matematica: la distinzione tra il linguaggio in cui si parla e ciò di cui si parla, la considerazione dei termini e delle formule come oggetti reali separati dalla loro denotazioni, la possibilità di ragionare matematicamente a entrambi i livelli.
Lo studio della logica tuttavia è quasi ovunque bandito dal filone principale dei curricula matematici, con diverse conseguenze negative, una delle quali riguarda proprio la comprensione corretta della teoria degli insiemi.
Le presentazioni di una teoria ingenua, o informale (naive set theory) sono infide, perché inevitabilmente selettive negli argomenti che riescono a coprire, per quanto possano essere ben meditate. Non si vede perché debba esistere una teoria degli insiemi naive e non un’algebra naive o una analisi naive.
Naive Set Theory è il titolo infelice e ambiguo di un fortunato e bel libro di Paul Halmos. Il libro è dedicato alla teoria assiomatica degli insiemi, ma non formalizzata. Halmos avrebbe preteso che il suo termine naive fosse chiaro e di senso univoco, o individuasse un nuovo stile, come mostra il suo apprezzamento per il fatto che la traduzione tedesca conserva nel titolo l’aggettivo come neologismo, ma così non è. In altri settori, come la fisica naive, il termine denota una impostazione non educata, diversa da quella scientifica. Non pare sia questa l’intenzione di Halmos: “naive” significa per lui soltanto che, come per ogni teoria non formalizzata, non viene descritta, né usata, ma neanche studiata, la sintassi del linguaggio.
La teoria degli insiemi è considerata l’erede dei sistemi come quelli di Gottlob Frege (1848–1925) e di Bertrand Russell (1872–1970), che ambivano a una fondazione logica della matematica. Questi tentativi sono considerati falliti, nella loro ambizione di definire tutti gli enti matematici solo in termini logici, dimostrandone anche l’esistenza logica. La teoria degli insiemi sarebbe allora per i filosofi un ripiego con meno pretese, ma pur sufficiente per le esigenze dei matematici, in quanto si accontenterebbe di postulare quello che serve per le loro costruzioni, troncando la ricerca all’indietro delle giustificazioni.
Le discussioni sullo stato della teoria degli insiemi come proposta fondazionale non sono esaurite. Ma quest’aura filosofica non ne facilita la fruizione didattica, vuoi per le riserve di chi la considera fuori dalla matematica, vuoi per la preoccupazione di chi la considera troppo difficile, comunque lontana dai problemi dell’insegnamento ,insincera o pelosa che sia questa ritrosaggine.
Eppure esiste una teoria degli insiemi, con un contenuto matematico ben definito, e con origini e motivazioni che risalgono a esigenze intrinseche allo sviluppo della matematica.
Se si volesse riassumere in una parola il campo della teoria si potrebbe dire che è lo studio (matematico) dell’infinito. Il che comporta – non ci si lasci turbare dalla grandezza del tema – che per complemento sia anche lo studio del finito. Dal che discende un interesse specifico non solo culturale degli insegnanti per il contenuto di questa teoria.
Continuiamo a menzionare in particolare gli insegnanti, tra i laureati in matematica, perché sono quelli più abbandonati a sé stessi.
L’esposizione che segue si propone come un aiuto a chi individualmente voglia colmare una grave lacuna della sua cultura. Naturalmente per imparare qualsiasi argomento bisogna studiare, in modo sistematico, svolgendo le dimostrazioni e risolvendo gli esercizi. I libri di testo e i corsi dedicati servono a questo scopo.
La storia
Le radici della teoria degli insiemi affondano in un terreno squisitamente matematico, e in un terreno importante, anzi proprio quello che viene comunemente chiamato mainstream della disciplina, precisamente nello studio delle funzioni.
Il primo libro nel quale sono stati presentati gli elementi della nascente teoria degli insiemi è il trattato di Emile Borel (1871–1956) del 1898 intitolato “Teoria delle funzioni”. Nella prima relazione generale sulla teoria degli insiemi, commissionatagli dalla Deutsche Mathematische Vereinigung, Arthur Moritz Schoenflies (1853–1928) vedeva la sorgente della teoria nel tentativo di chiarificazione di due concetti collegati, quello di argomento e quello di funzione. Per il primo, equivalente a quello di variabile indipendente, egli notava come fosse stato a lungo legato al concetto intuitivo e non ulteriormente definito del continuo geometrico, mentre ora gli argomenti variavano su insiemi di valori o di punti qualunque. Per quel che riguarda il concetto di funzione, Schoenflies tracciava le grandi linee della evoluzione ottocentesca, a partire da Fourier (J.-B. Joseph Fourier, 1768–1830) e dalla sua affermazione che una funzione arbitraria può essere rappresentabile da una serie trigonometrica; dava il giusto rilievo alla definizione di Dirichlet (Gustav Lejeune Dirichlet, 1805–1859), in cui il concetto generale di funzione è equivalente, detto in breve, a quello di una Tabelle arbitraria, antesignano della moderna definizione insiemistica; ricordava come l’esempio di Bernhard Riemann (1826–1866) di una funzione rappresentabile analiticamente ma discontinua in ogni punto razionale e continua in ogni punto irrazionale avesse messo i matematici di fronte a possibilità per fondare
le quali le rappresentazioni disponibili non erano sufficienti. Nello studio generale delle proprietà delle funzioni, e in particolare della loro rappresentazione in serie, si era venuti a considerare come critici i punti di discontinuità o di minimo o massimo; si ricordi che nel Settecento una funzione con una discontinuità di prima specie in un punto, o con un punto di non derivabilità, o comunque definita da due espressioni diverse in due sottointervalli non era propriamente considerata una funzione, ma due. Quando si passò a considerare infiniti punti critici fu immediatamente evidente il ruolo cruciale della loro distribuzione spaziale, e iniziò lo studio degli insiemi infiniti di punti sulla retta, il vero inizio della teoria degli insiemi. Il primo lavoro di Georg Cantor (1845–1918) riguardava l’unicità della rappresentazione di Fourier per funzioni prima con un numero finito e poi con un numero infinito di punti critici.
Topologia della retta
Nello studio degli insiemi di punti Cantor mise le basi della topologia della retta, introducendo il concetto di insieme derivato (insieme dei punti di accumulazione) di un insieme, quindi quelli di insieme chiuso, perfetto, denso in sé, isolato, l’aderenza e la coerenza di un insieme e così via. Altri analisti contribuirono a questo arricchimento, Paul du Bois-Reymond (1831–1889) e Hermann Hankel (1839–1873) tra gli altri. Ma Cantor aveva uno strumento da lui inventato che gli permetteva uno studio più fine e più fecondo, l’iterazione transfinita dell’insieme derivato.
Nello stesso tempo che elaborava i concetti e i risultati matematici Cantor doveva inventare la terminologia e costruire il linguaggio; ad esempio furono introdotti allora per la prima volta simboli speciali per l’unione e per l’intersezione, e in seguito per il prodotto, anche se diversi da quelli ora universalmente adottati. La stessa parola “insieme” non era di uso consolidato, in tedesco si usava Menge ma anche Punktmannigfaltigkeit, o varietà di punti, in italiano “aggregato” o “gruppo”.
Numeri infiniti
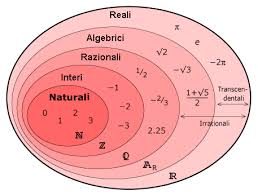
Gli argomenti che hanno fatto diventare matematica e indipendente la teoria degli insiemi sono tuttavia altri, e precisamente i cardinali e gli ordinali infiniti. La elaborazione di questa teoria non è un seguito diretto dello studio degli insiemi di punti della retta, anche se trova ivi la sua motivazione e le sue origini. Gli insiemi di punti non sono insiemi astratti nel senso che verrà a stabilirsi, ma insiemi i cui elementi sono oggetti matematici supposti già definiti e conosciuti in modo indipendente o prioritario, i numeri reali in questo caso. I cardinali e gli ordinali infiniti non c’erano ancora. Per arrivare ad essi Cantor ha avuto l’intuizione creativa di considerare insiemi astratti, o insiemi in sé, prescindendo dalla natura dei loro elementi. Prima della introduzione dei numeri cardinali infiniti peraltro, la scoperta della possibilità di considerare infiniti diversi, di diversa potenza, nasce in Cantor con la dimostrazione che l’insieme dei numeri naturali e l’insieme dei numeri reali non possono essere messi in corrispondenza biunivoca, di nuovo un fatto di genuino interesse analitico. Invece con i numeri naturali possono essere messi in corrispondenza biunivoca i numeri razionali, come anche (ed è stata per molti una sorpresa) i numeri algebrici.
Per il risultato sui reali Cantor, dopo una prima dimostrazione che sfruttava la continuità della retta, ha inventato il metodo diagonale, con una formulazione astratta che non dipende dalla natura degli enti e sarà quindi generalizzabile. Secondo Schoenflies, la teoria degli insiemi è diventata una disciplina matematica proprio quando Cantor ha presentato il numerabile (cioè la cardinalità dell’insieme dei numeri naturali) come un ben definito concetto matematico, insieme alla classificazione degli insiemi infiniti secondo la potenza, e con la dimostrazione che i numeri algebrici sono numerabili, mentre il continuo non lo è. La cardinalità definita con le corrispondenze biunivoche rivelava comportamenti inaspettati dell’infinito – al di là del fenomeno da lungo tempo notato come non più che una curiosità, che il tutto può essere equivalente a una sua parte – quale l’equipotenza del quadrato e di un suo lato. Le prime osservazioni riguardavano sempre il continuo dei numeri reali. Per generalizzare, occorreva come si è detto un salto logico, quello di non considerare più gli insiemi, come erano stati fino ad allora, solo uno strumento linguistico – analogo ai predicati – di analisi di una realtà particolare autonoma oppure come un modo di riferirsi ai sistemi numerici abituali nella loro totalità – l’insieme dei numeri interi, razionali, . . . – ma come un concetto in sé.
(1900)