Vado al massimo!

Problemi di minimo e massimo

“Il numero del mio taxi è il 1729, mi sembra un numero alquanto stupido”. Al che Ramanujan rispose: “No Hardy! No! E’ un numero molto interessante. E’ il numero più piccolo esprimibile come la somma di due cubi in due diversi modi: 1729 = 10^3 + 9^3, 1729 = 12^3 + 1^3.

Srinivasa Ramanujan

I problemi di minimo e di massimo hanno stimolato e affascinato gli scienziati fin da tempi remoti, tanto da farcene trovare già nelle opere dei matematici greci del III secolo a.C. Possiamo trovare esempi  in ambito geometrico e fisico, come la determinazione delle rette di lunghezza minima e massima che possono essere condotte a una conica da particolari punti; la determinazione del percorso che sceglie un raggio di luce che viene emesso in un punto, riflesso da uno specchio e raggiunge un punto finale; il problema della brachistocrona, cioè quello di determinare la curva che rappresenti il percorso che un corpo compie per andare da un punto ad un altro, lungo un piano verticale, nel minor tempo possibile; il problema isoperimetrico, cioè quello di determinare tra tutte le figure con lo stesso perimetro quella che racchiuda area massima, e molti altri. Questi problemi sono affrontati con diversi metodi che si sono evoluti nel tempo: mentre nell’antichità le tecniche sfruttate per la risoluzione sono puramente geometriche, come vedremo attraverso l’analisi dei risultati di Euclide, Archimede, Apollonio, Zenodoro ed Erone, nei secoli XVII-XVIII viene impresso un forte impulso al loro studio dalla nascita di metodi infinitesimali, con la produzione di lavori sull’argomento da parte di Fermat, Huygens, i fratelli Bernoulli, fino alle fondamentali opere di Leibniz, Eulero e Lagrange.

 Il problema di Didone

Il primo problema di massimo nella storia è un’antica leggenda riportata perfino nel Libro I dell’Eneide di Virgilio.
Nel IX secolo a.C. la principessa di Tiro, Didone, dopo l’uccisione del marito Sicheo per mano del fratello Pigmalione, fugge per mare insieme alla sorella e ad un vasto seguito; arrivata sulle coste libiche chiede al re Iarba un pezzo di terra su cui fondare la città: ”taurino quantum possent circumdare tergo” (quanta una pelle di bue ne potesse circondare, Eneide, I, 367-368); il re acconsente e lei riesce a ottenere la terra necessaria per costruire una fortezza e fondare la città di Cartagine.
Come ha fatto? Didone, con un paio di forbici, ha tagliato la pelle di bue in strisce sottilissime con le quali ha formato un filo abbastanza lungo da poter circondare un’ampia zona.
Che forma ha dato a questo filo? Didone voleva uno sbocco sul mare quindi ha fissato le due estremità del filo e gli ha dato la forma di una semicirconferenza.

Questo aneddoto è noto come problema di Didone ed è il classico problema isoperimetrico: fra tutte le curve piane di lunghezza data (cioè isoperimetriche, iso: stesso), qual è quella che racchiude la massima area?
Il problema in questione, in realtà, ha una soluzione abbastanza difficile; i Greci avevano capito che questa era rappresentata dalla circonferenza (infatti Virgilio utilizza la parola ”circumdare”, che ci fa dedurre che Didone avesse risolto in modo corretto il problema); analogamente avevano notato la proprietà isoepifanica della sfera (ossia, tra tutte le figure con uguale superficie, la sfera è quella di volume massimo). Proprio per questa proprietà di ”massima capienza” nello spazio e nel piano, la sfera e il cerchio erano viste come la materializzazione della perfezione geometrica. E’ impossibile dire con precisione chi abbia notato per primo questa proprietà; quello che però è noto è che Aristotele nel IV secolo a.C. la tratta come un fatto assodato.
In ogni caso, gli antichi non avevano una dimostrazione rigorosa (per i nostri standard) di questo fatto; tra i solutori del problema, secondo gli standard del tempo, ricordiamo Archimede e Zenodoro, di cui parleremo più avanti.

 Euclide

Il primo problema di massimo esplicitamente formulato è contenuto nel Libro VI degli Elementi di Euclide, matematico alessandrino del III secolo a.C. In quest’opera Euclide raccoglie e sistema in modo assiomatico tutto il sapere matematico fino ad allora disponibile e ci offre il primo esempio di ”trattato scientifico”, per il metodo rigorosamente deduttivo utilizzato.
(Proposizione XXVII). Di tutti i parallelogrammi applicati alla stessa retta e deficienti di figure parallelogrammiche sia simili sia poste similmente a quella descritta sulla metà della retta, è massimo quel parallelogrammo che è applicato sulla metà della retta ed è simile al difetto.

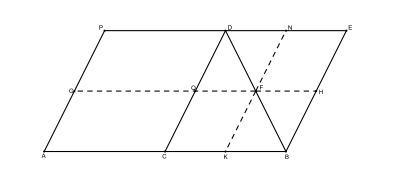
In termini moderni, potremmo enunciare questa proposizione nel seguente modo:
dato un triangolo ABC, se da un punto D del lato BC si tracciano le parallele ED ad AC, FD ad AB, l’area del parallelogramma AEDF è massima quando D è il punto medio di BC.

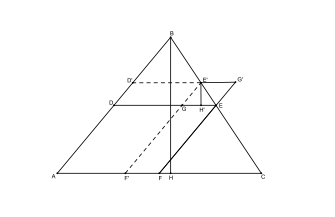
Archimede

L’opera Sulla sfera e sul cilindro di Archimede, matematico, fisico e inventore siracusano del III secolo a.C., può essere considerata come la diretta continuazione degli Elementi di Euclide, in quanto riparte proprio da dove quest’ultimo termina: i cosiddetti solidi di rotazione.
Sulla sfera e sul cilindro è un’opera in due libri, ognuno preceduto da una lettera introduttoria di Archimede stesso al matematico alessandrino Dositeo.
Nel primo libro troviamo i noti risultati riguardanti la superficie e il volume della sfera, mentre il secondo libro è molto diverso: si potrebbe quasi dire che Archimede abbia qui raccolto e risolto, sotto la spinta di Dositeo, dei problemi abbastanza difficili da lui già proposti ai geometri di Alessandria.
La proposizione più  interessante (per l’argomento che stiamo affrontando) è la IX del Libro II:

(Proposizione II, IX). Tra tutti i segmenti sferici compresi da uguale superficie, il maggiore è l’emisfero.
La proposizione così posta risolve il problema di massimo: tra tutti i segmenti sferici aventi uguale superficie, trovare quello di massimo volume; naturalmente si intende che i segmenti sferici da confrontare possano appartenere a sfere diverse.

Galilei

Ebbene, anche Galileo entra nell’ argomento dei massimi e minimi e dimostra:
(1) Il cerchio è medio proporzionale tra qualsivoglino due poligoni regolari tra  di loro simili, de i quali uno gli sia circoscritto e l’altro gli sia isoperimetrico;
(2) In oltre, essendo egli minore di tutti i [poligoni] circoscritti, è all’incontro massimo di tutti gli isoperimetrici;
(3) De i medesimi poi circoscritti, quelli che hanno più angoli sono minori di quelli che ne hanno manco; ma all’incontro de gl’isoperimetrici quelli di più angoli son maggiori.
Per dimostrare questo, Galileo si serve implicitamente di alcuni risultati di Euclide che mettiamo in evidenza ed anche, ecco un altro contatto con Archimede, di una proposizione tratta dalla Misura del cerchio.

 Zenodoro

”I poligoni regolari hanno area massima tra tutti i poligoni con egual perimetro e numero di lati.”
”Il cerchio ha area maggiore di qualsiasi poligono regolare di egual perimetro.”
Tra il III e il I secolo a.C. Zenodoro, matematico e astronomo probabilmente ateniese, scrive l’opera Sulle figure isoperimetriche, contenente tra l’altro la dimostrazione delle due proposizioni sopra citate. Purtroppo questo
libro, che può considerarsi la prima opera scientifica dedicata al problema isoperimetrico, è andato perduto; fortunatamente, però, si è potuto ricostruirne il contenuto attraverso il Libro V delle Mathematicae Collectiones di Pappo e ad un trattato nel commentario di Teone al I libro dell’Almagesto di Tolomeo.
Pappo, matematico alessandrino del IV secolo d.C., con le sue Collectiones, opera in otto volumi, voleva produrre un compendio di tutta la matematica fino ad allora conosciuta. In particolare, nel Libro V compara le aree di figure piane differenti con lo stesso perimetro seguendo proprio il trattato di Zenodoro; inoltre compara anche i volumi di solidi diversi con la stessa area superficiale.

I ragionamenti di Zenodoro hanno segnato profondamente il modo di affrontare il problema isoperimetrico, tanto che fino alla fine del XVII secolo si trovano ripetuti più o meno fedelmente. Il primo matematico che ha apportato
delle innovazioni importanti alla questione è stato Jakob Steiner nel 1800, il quale inventò delle tecniche per dimostrare che ogni figura d’assegnato perimetro che racchiuda la massima area deve essere necessariamente un
cerchio. Le tecniche di Steiner si basano su un semplice principio: sia S una figura piana d’area massima, se S non è un cerchio si può trovare un’altra figura piana T isoperimetrica a S ma che abbia area maggiore. Tuttavia anche Steiner lasciò una questione irrisolta: come fece notare Dedekind non si pone il problema dell’esistenza della soluzione del problema isoperimetrico.
La teoria di Steiner fu perfezionata ad inizio ’900 da Wilhelm Blaschke, il quale dimostrò l’esistenza di una figura con area massima usando un teorema di compattezza nella classe delle figure convesse.
La questione dell’esistenza rimase aperta fino alla fine del XIX secolo, quando Weierstrass propose una dimostrazione variazionale piuttosto generale dell’esistenza di figure di area massima. Dopo di lui, nel XX secolo, la Teoria della Misura di Lebesgue cambiò in modo radicale l’approccio alle questioni riguardanti le aree e i perimetri, in quanto la nozione di misura secondo Lebesgue consentiva di misurare l’area di molti più insiemi (si notò subito che la misura di Lebesgue era una generalizzazione del classico concetto di area della geometria elementare). Per trovare una definizione altrettanto generale di perimetro che consentisse di misurare la lunghezza del bordo di insiemi particolarmente bizzarri bisognò aspettare gli anni ’50 del XX secolo, quando Ennio De Giorgi riprese ed elaborò le idee di Caccioppoli e giunse alla dimostrazione dell’esistenza di soluzioni del problema isoperimetrico generale:
”tra tutte le figure piane aventi perimetro di De Giorgi assegnato, determinare quelle aventi misura di Lebesgue massima”.
Adattando i ragionamenti di Steiner, dimostrò che queste figure sono necessariamente cerchi e questo vale in un qualsiasi spazio a dimensione finita.

Erone

Erone di Alessandria, matematico greco del I secolo d.C., interessato all’ottica e alla meccanica, ha scritto l’opera Catottrica, andata persa, ma di cui conosciamo gli argomenti trattati attraverso i commentari successivi in cui viene descritta.
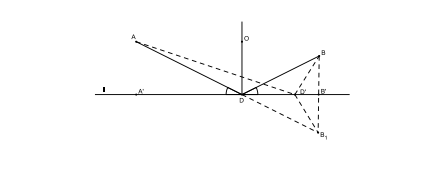
In questo testo Erone ipotizza che la luce scelga sempre il percorso più breve come distanza per andare da un punto ad un altro; in questo modo riesce a dimostrare la legge della riflessione della luce: un raggio di luce proveniente da un punto A e incidente su uno specchio piano l in un punto D, viene riflesso nella direzione di un punto B tale che AD e BD formino con l angoli uguali. In pratica Erone dimostra che, fra tutti i cammini possibili per andare da A a B passando per lo specchio, il cammino più breve è quello per cui gli angoli di incidenza e riflessione sono uguali.

(272)