
Indice
Sistemi simmetrici
Definizione
Un sistema di due equazioni in due incognite si dice simmetrico se rimane lo stesso scambiando tra loro le incognite.
Per esempio, se nel sistema

che è identico al precedente.
Risolviamo il sistema, le soluzioni sono
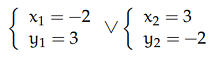
e come si può notare x e y vengono scambiate anche nella soluzione.
In generale, se il sistema è simmetrico, trovata una coppia soluzione (a; b) l’altra è (b; a).
Sistema simmetrico fondamentale
Il sistema simmetrico fondamentale è del tipo

e risolve il problema di trovare due numeri, nota la loro somma e il loro prodotto.
Ricordiamo che nell’equazione di secondo grado
x2 + bx + c = 0
la somma delle radici è −b, mentre il prodotto è c.
Pertanto, basta risolvere l’equazione t2 − st + p = 0, detta equazione risolvente.
In base al segno del discriminante ∆ = s2 − 4p
abbiamo:
➡ ∆ > 0: l’equazione risolvente ha due soluzioni distinte t1 e t2, le soluzioni del sistema sono:

➡ ∆ = 0: l’equazione risolvente ha radici coincidenti t1 = t2, le soluzioni del sistema sono:

➡ ∆ < 0: l’equazione non ammette soluzioni reali. Il sistema è impossibile.
Esercizio 1
Risolvere il seguente sistema:

Soluzione
L’equazione risolvente è
t2 − t + 4 = 0
che ha il discriminante negativo e dunque non ha soluzioni reali. Il sistema è impossibile.
Possiamo interpretare i risultati ottenuti nel piano cartesiano:
la retta di equazione x + y = 1 non interseca mai l’iperbole equilatera xy = 4

Esercizio 2
Risolvere il seguente sistema:

Soluzione
Otteniamo l’equazione risolvente:
t2−10t + 21=0
Troviamo le soluzioni dell’equazione risolvente:
t1=3 ∨ t2=7
Le soluzioni del sistema sono le seguenti:

Possiamo interpretare i risultati ottenuti nel piano cartesiano: la retta di equazione x+ y=10 interseca l’iperbole equilatera xy=21 nei due
punti A(7;3) e B(3,7)

Sistemi simmetrici riconducibili al sistema simmetrico fondamentale
In questa categoria rientrano i sistemi simmetrici che, mediante artifici algebrici, possono essere trasformati, in modo equivalente, in sistemi simmetrici del tipo precedente.
Esempio 1
![]()
È possibile trasformare il sistema in un sistema simmetrico fondamentale.
Ricordando l’identità:
![]()
Esercizio 3
Risolvere il seguente sistema:
![]()
Soluzione
Ricordando l’identità:
x2 + y2 = (x + y)2 -2xy
il sistema può essere riscritto così:
![]()
Sistemi non simmetrici riconducibili a sistemi simmetrici
Rientrano in questa classe i sistemi che, pur non essendo simmetrici, possono essere trasformati, mediante opportune sostituzioni, in sistemi simmetrici. Naturalmente questi sistemi si possono risolvere anche con la procedura solita di sostituzione per i sistemi di secondo grado.
Esempio
![]()
Mediante la sostituzione y ‘=−y otteniamo:
![]()
(1599)
