Le funzioni iperboliche

Le funzioni iperboliche sono funzioni speciali dotate di proprietà formalmente simili a quelle di cui sono dotate le funzioni goniometriche ordinarie. Anche la loro definizione in termini geometrici è molto simile alla definizione in termini geometrici delle funzioni goniometriche ordinarie.

I nomi di tali funzioni sono scelti in modo da richiamare immediatamente tali somiglianze formali.

Definizione geometrica delle funzioni goniometriche

Le funzioni goniometriche (senx, cosx, tanx, cscx, secx, cotx, per citare soltanto le principali) possono essere tutte introdotte a partire dalla circonferenza goniometrica, ovvero la circonferenza di raggio unitario centrata nell’origine di un sistema di assi cartesiano.
Ad esempio, data la circonferenza goniometrica di equazione X² + Y² = 1 e tracciato il raggio OP a distanza angolare α dalla direzione positiva dell’asse X, cosα e senα sono definiti rispettivamente come l’ascissa e l’ordinata del punto P; per tanα è necessario tracciare la retta tangente alla circonferenza nel punto (1,0); per cotα è necessario tracciare la retta tangente alla circonferenza nel punto (0,1); e così via…

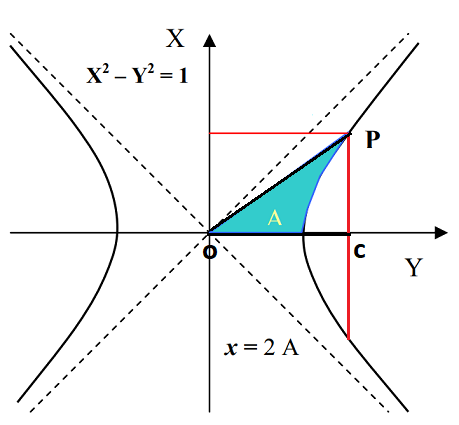
Definizione geometrica delle funzioni iperboliche

Similmente introduciamo le funzioni iperboliche, usando stavolta l’iperbole equilatera centrata nell’origine di semiassi unitari a = b =1, avente quindi come equazione

X²–Y² = 1

e come asintoti le rette bisettrici dei quadranti.
Impiegheremo uno solo dei due rami di cui l’iperbole è composta: diciamo quello di equazioni

per X ≥ 1.

Dato un numero reale x, sia P il punto sul nostro ramo di iperbole che individua il settore iperbolico di areaΑ = x / 2.

Si definiscono coseno iperbolico coshx e seno iperbolico senhx rispettivamente l’ascissa e l’ordinata del punto P.

L’area del settore iperbolico è presa positiva (o negativa) se P ha ordinata positiva (o negativa). Nella figura è mostrato in celeste il settore iperbolico, di area Α, corrispondente al punto P sul ramo di iperbole; il doppio della sua area è indicato con il simbolo x. Stavolta non è possibile parlare di angolo α per avere una definizione di seno e coseno iperbolici con insieme di definizione R: questo perché il segmento OP presenta sempre apertura angolare rispetto all’asse X limitata nell’intervallo (– π/ 4, π/ 4)!

Ci si potrebbe allora chiedere se la definizione in termini di area del settore iperbolico conduca a funzioni iperboliche definite su tutto l’insieme dei numeri reali R; ovvero se l’area del settore iperbolico continui a crescere all’infinito, in valore assoluto, qualora l’ascissa del punto P cresca all’infinito, oppure se essa converga ad un certo valore estremo.
Vedremo fra un attimo che l’area Α = x / 2 del settore iperbolico non è limitata, dunque Α ∈ (–∞, +∞).

Espressioni analitiche in termini di esponenziali

Ci chiediamo: è possibile derivare espressioni analitiche per il seno iperbolico e il coseno iperbolico (appena definiti per via geometrica) in termini di altre funzioni note semplici? Sì, è possibile.

Il coseno iperbolico

Sia l’ordinata di P positiva (identico l’altro caso). L’area Α del settore iperbolico OAP è pari alla differenza tra l’area del triangolo OPC e l’area della regione di piano delimitata dall’arco di iperbole AP, dall’asse X e dal segmento PC.
Possiamo dunque scrivere, ricordando che il vertice A dell’iperbole è il punto (1,0):

 

Ecco qua la giustificazione di cui necessitavamo per la nostra trattazione: l’area Α, ossia la variabile da cui abbiamo fatto dipendere per definizione il seno iperbolico e il coseno iperbolico, non ha limitazioni!

Per X ≥ 1 e Y_P ≥ 0 si ha Α ≥ 0, mentre nel caso X ≥ 1 e Y_P ≤ 0 si avrà Α ≤ 0.

Dunque il dominio per seno e coseno iperbolici è proprio tutto R! Prendiamo allora il logaritmo come nostra futura variabile indipendente
e poniamo

Il seno iperbolico

Potremmo seguire il medesimo procedimento, calcolando ancora l’area del settore iperbolico OAP facendo comparire l’ordinata Y del punto P mediante la sostituzione

 

(sempre nell’ipotesi Y_P ≥ 0; similmente nel caso Y_P ≤ 0). Tuttavia non sarebbe più istruttivo del calcolo appena fatto: deduciamo perciò il seno iperbolico ricordando che il punto P appartiene all’iperbole per cui le sue coordinate soddisfano la condizione  X²– Y²= 1.

Per Y_P ≥ 0 si ha x = 2Α ≥ 0,

poiché e^x ≥ e^-x ;

per Y_P ≤ 0 si ha x = 2Α ≤ 0,

poiché e^x ≤ e^-x ;

Riassumendo, per ogni punto P (e quindi per ogni area Α)

(375)