Studio di funzioni razionali fratte
Studiare le seguenti funzioni FINO alla derivata prima, tracciarne il grafico ed indicare gli eventuali punti di minimo e massimo (sono locali o assoluti?).
ESERCIZIO 1:

SOLUZIONE:
Classificazione.
E una funzione razionale fratta, poichè la variabile indipendente x compare anche al denominatore della frazione.
Dominio.
Poichè nella funzione compare una frazione, per determinarne il dominio bisogna porre la condizione che il denominatore sia diverso da zero, e pertanto si deve avere:
x2 + x − 2 ≠ 0 ⇒ x ≠ −2; x ≠ 1
Il dominio della funzione è
Df = ] − ∞; −2[ ∪ ] − 2; 1[ ∪ ]1; +∞[
Intersezioni con gli assi.
Con l’asse y abbiamo:

Con l’asse x abbiamo:
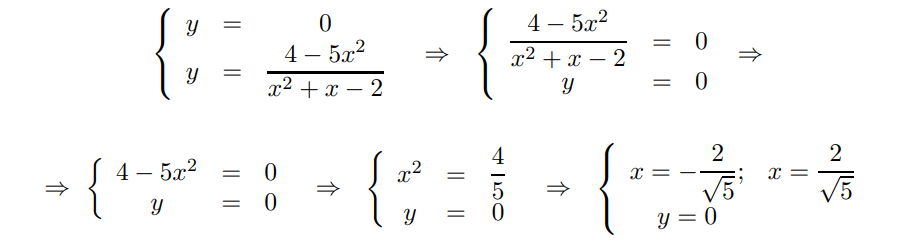
Pertanto la funzione interseca gli assi nei punti di coordinate:

Segno:
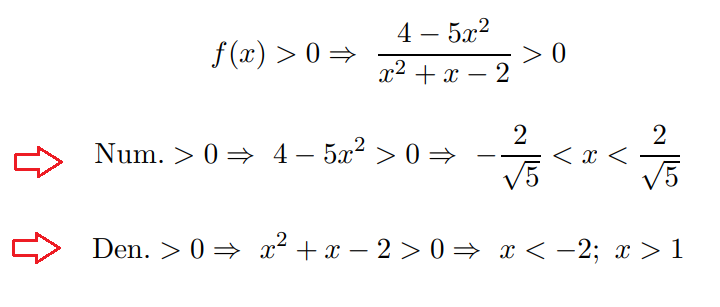
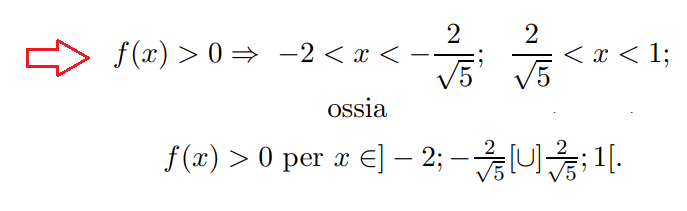
Comportamento della funzione in punti particolari del dominio.
I punti importanti, per i quali è utile stabilire il comportamento della funzione, sono −2, 1, −∞, +∞.
Abbiamo che:

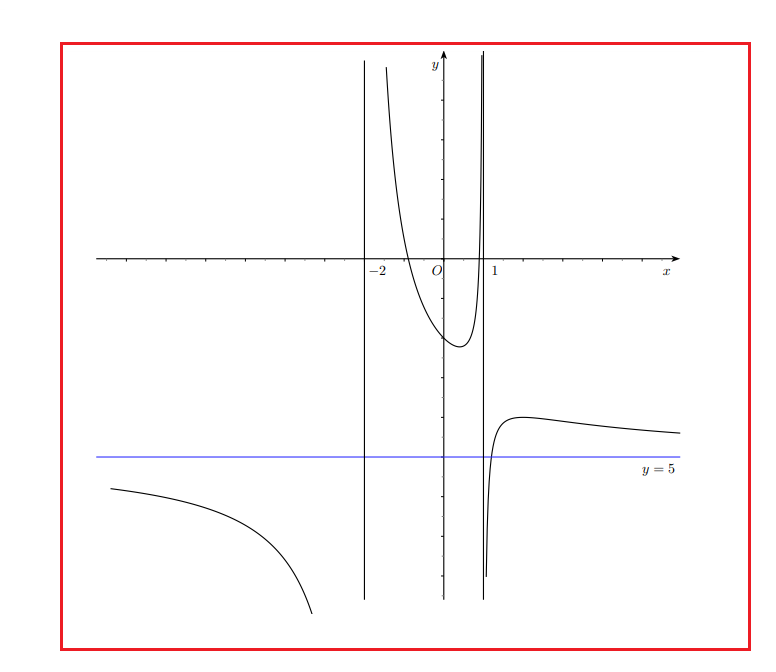
Avendo ottenuto due risultati infiniti per x tendente ad un valore finito (da destra e da sinistra), si può concludere che la retta di equazione
x = −2 è un asintoto verticale per la funzione.
Abbiamo che:
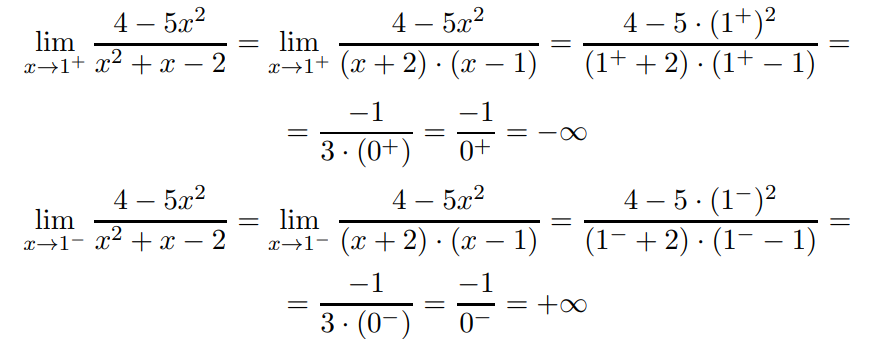
Avendo ottenuto due risultati infiniti per x tendente ad un valore finito (da destra e da sinistra), si può concludere che
la retta di equazione x = 1 è un asintoto verticale per la funzione.

Possiamo concludere che la funzione ammette come asintoto orizzontale la retta
y = −5.
Studio della derivata prima.
Abbiamo che:

Possiamo concludere che:

IL GRAFICO:

ESERCIZIO 2:
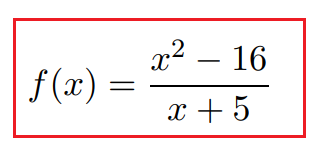
Classificazione.
E una funzione razionale fratta, poichè la variabile indipendente x compare anche al denominatore della frazione.
Dominio.
Poichè nella funzione compare una frazione, per determinarne il dominio bisogna porre la condizione che il denominatore sia diverso da zero, e pertanto si deve avere:
x + 5 ≤ 0 ⇒ x≤ −5.
Il dominio della funzione è Df = ] − ∞; −5[∪] − 5; +∞[
Intersezioni con gli assi.
Con l’asse y abbiamo:

Con l’asse x abbiamo:

Segno

Comportamento della funzione in punti particolari del dominio.
I punti importanti, per i quali è utile stabilire il comportamento della funzione, sono −5, −∞, +∞.
Abbiamo che:
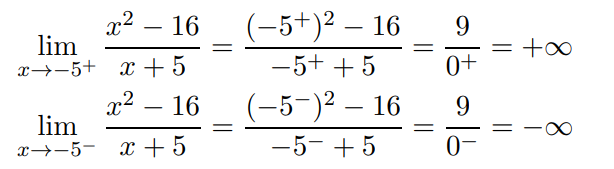
Avendo ottenuto due risultati infiniti per x tendente ad un valore finito (da destra e da sinistra), si può concludere che
la retta di equazione x = −5 è un asintoto verticale per la funzione.

Similmente si ha:

Calcolando i limiti per x tendente all’infinito si sono ottenuti valori infiniti: di conseguenza si può affermare che la funzione non ammette asintoto orizzontale, allora vediamo se esiste l’asintoto obliquo.
La funzione ammette come asintoto obliquo la retta y = mx + q se esistono finiti i seguenti limiti:
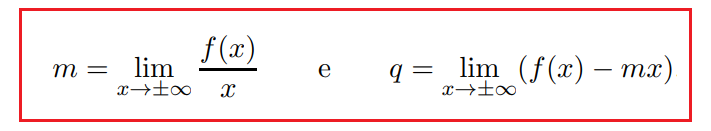
Abbiamo che

Analogamente:
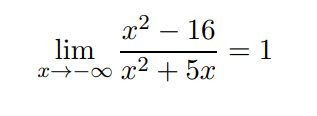
Dunque m = 1.
Infine, abbiamo che

Similmente si ha:

Dunque q = −5. Possiamo concludere che la funzione ammette come asintoto obliquo la retta y = x − 5.
Studio della derivata prima.
Abbiamo che:
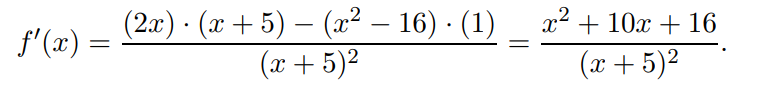
Studiamo il segno della derivata prima:


Grafico probabile.

Altri studi di funzione
[elementor-template id=”10428″]
(26414)
