
Indice
Breve ripasso:
Cosa sono le esponenziali
Le equazioni esponenziali
Si chiamano equazioni esponenziali tutte le equazioni che contengono un valore incognito all’esponente. Le più semplici in cui ci si può imbattere
sono dette elementari e si presentano nella forma:
ax = b
con a > 0; a ≠ 1.
Quante soluzioni ha questa equazione?
Poichè ax è un numero sempre positivo, l’equazione risulterà impossibile se b≤ 0.
L’equazione ha invece un’unica soluzione con b > 0. Per risolvere le equazioni elementari vanno ricordate e applicate le proprietà delle potenze e la definizione di logaritmo.
Proprietà delle potenze
Per ogni opportuna scelta dei numeri reali a; b; c, valgono le seguenti proprietà:

Come si procede se l’equazione esponenziale non è elementare?
I casi più frequenti sono tre :
1) Nei due membri dell’equazione compaiono solo prodotti e quozienti di potenze con la stessa base.
Ci si può ricondurre a una forma del tipo:
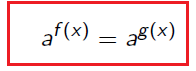
Si Ricorda che la condizione a > 0 va imposta perchè una potenza ad esponente reale ha senso solo se la base è un numero reale positivo.
Poichè in questo caso abbiamo un’uguaglianza fra due potenze con la stessa base, l’uguaglianza sussiste solo se anche gli esponenti
coincidono, cioè f(x) = g(x)
2) Compaiono esponenziali con due basi diverse ma stesso esponente.
Applicando le proprietà delle potenze si può ridurre l’equazione a una forma del tipo:
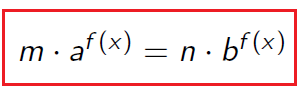
Poichè la potenza di un numero reale positivo è sempre maggiore di zero, bf(x) ≠ 0 ∀ x ∈ R, quindi posso dividere ambo i membri per bf(x) ,si ritrova un’equazione elementare:

Esempio:

3) L’equazione contiene ax e il suo quadrato a2x .
Tramite la sostituzione t = ax si può trasformare l’equazione in un’equazione di secondo grado nella variabile t; risolta questa, si riconduce la soluzione a un’equazione esponenziale elementare.

e si risolve l’equazione di secondo grado in t.
Esempio:

Esercizio 1

Esercizio 2

Esercizio 3

Esercizio 4

Esercizio 5

Esercizio 6

Equazioni esponenziali risolvibili coi logaritmi
Alcune equazioni esponenziali si possono risolvere applicando il logaritmo ad entrambi i membri e sfruttando le proprietà dei logaritmi.
Esercizio 7

Esercizio 8

(20097)
