
Indice
Disequazioni in cui sono presenti valori assoluti
Esercizio 1
Risolvete la seguente disequazione:
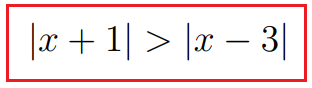
Soluzione
La soluzione è x > 1.
Infatti si distinguono tre casi:
x < −1,
−1 ≤ x ≤ 3,
x > 3.
Si ha:

Mettendo assieme i risultati dei vari sistemi si ottiene la soluzione data.
Esercizio 2
Risolvete la seguente disequazione:

Soluzione
La soluzione è x < −3 ∨ x > 1.
Infatti si distinguono tre casi:
x < 0,
0 ≤ x ≤ 3,
x > 3.
Si ha:

Mettendo assieme i risultati dei vari sistemi si ottiene la soluzione data.
Equazioni con radicali
Esercizio 3
Risolvete la seguente equazione:

Soluzione
La soluzione è x ≥ 2.
Infatti innanzitutto bisogna porre l’esistenza delle radici, quindi bisogna mettere a sistema
x2 − 4 ≥ 0,
x − 2 ≥ 0 e
x + 2 ≥ 0
che dà x ≥ 2.
A questo punto si semplificano ambo i membri per cui l’equazione data diventa un’identità, ragion per cui ogni x che soddisfa le condizioni di esistenza delle radici va bene.
Esercizio 4
Risolvete la seguente equazione:

Soluzione
La soluzione è x = 6 − 2√3.
Infatti innanzitutto bisogna porre l’esistenza della radice, quindi x ≥ 2.
D’altra parte, siccome sto uguagliando un secondo membro a una radice, che è sempre positiva (o nulla), devo porre l’ulteriore condizione che anche il secondo membro sia non negativo, altrimenti avrei un assurdo, quindi pongo anche
4 − x ≥ 0 cioè x ≤ 4.
Le condizioni sono dunque 2 ≤ x ≤ 4.
A questo punto elevo a quadrato ambo i membri e ottengo, dopo semplici calcoli, le soluzioni x = 6 ± 2√3;
scarto la soluzione x = 6 + 2√3 perché non rientra nell’intervallo individuato prima e ho la soluzione proposta.
Esercizio 5
Risolvete la seguente equazione:

Soluzione
La soluzione è x = 1.
Infatti innanzitutto bisogna porre l’esistenza della radice a destra cioè x ≤ 2; poi devo porre l’esistenza della radice a sinistra, cioè
3x − 2√x ≥ 0. Per risolvere quest’ultima prima pongo x ≥ 0 poi elevo a quadrato e ottengo 9x2 − 4x ≥ 0 che risolta dà x ≤ 0 ∨ x ≥ 4/9.
Mettendo a sistema le tre condizioni
x ≤ 2,
x ≥ 0 e
x ≤ 0 ∨ x ≥ 4/9
si ottiene la condizione 4/9 ≤ x ≤ 2. Ora posso elevare a quadrato nella mia equazione di partenza e ottengo 3x−2√x = 2−x che porta a
√x = 2x−1.
A questo punto, prima di elevare di nuovo al quadrato, occorre porre una nuova condizione di compatibilità, cioè 2x − 1 ≥ 0 (il secondo membro deve essere non negativo perché uguagliato a una radice) che messa a sistema con la precedente porta a 1/2 ≤ x ≤ 2.
Ora posso elevare finalmente a quadrato ambo i membri e ottengo l’equazione 4x2 − 5x + 1 = 0 che risolta dà:
x = 1 accettabile e
x = 1/4 non accettabile
per quanto detto sopra.
Equazioni con valore assoluto
Esercizio 6
Risolvete la seguente equazione:

Soluzione
La soluzione è: x = 1.
Infatti, si distinguono i tre casi: x < −1 che non dà soluzioni,
−1 ≤ x ≤ 3 che dà come soluzione x = 1
e infine x > 3 che non dà soluzioni.
Equazioni esponenziali
Esercizio 7
Risolvete la seguente equazione:

Soluzione
L’unica soluzione accettabile è:

Infatti si pone 3x = t; notare che deve essere t > 0, quindi se troverò t non positivi dovrò scartarli. Allora si deve risolvere t2−t−5 = 0 che fornisce le soluzioni

da cui la soluzione proposta.
Equazioni logaritmiche
Esercizio 8
Risolvete la seguente equazione:
![]()
Soluzione
x = 27.
Infatti basta ricordare che
1 = log3 3
da cui
log3 x = 3 log3 3 = log3 33
quindi x = 27.
Esercizio 9
Risolvete la seguente equazione:

Soluzione
x = 2.
Infatti basta prendere i logaritmi di ambo i membri, si ottiene

da cui x = 2 oppure x = −1; la soluzione x = −1 non è accettabile a causa delle condizioni di esistenza del logaritmo
(x > 0 e x > −1, da cui deve necessariamente essere x > 0).
Esercizio 10
Risolvete la seguente equazione:

Soluzione
x = 4. Infatti basta ricordare la
formula del cambiamento di base
e il fatto che log(ab) = log a + log b; quindi l’equazione di partenza si riduce a

(2030)

