Indice
I Logaritmi
DEFINIZIONE:
Sotto le condizioni
a>0, a≠1, b>0
l’equazione
ax = b
ammette un’unica soluzione; esiste cioè un numero x che messo ad esponente di b fornisce come risultato a. Questo numero viene detto logaritmo in base a di b e viene simbolicamente così rappresentato:
x = log a ( b)
I numeri a e b vengono rispettivamente chiamati base ed argomento del logaritmo dato.

Il logaritmo di un numero in una data base esiste soltanto se il numero e la base sono positivi e la base è diversa da 1.
Perchè a>0 ?
Le potenze ad esponente razionale e reale (nel campo reale) vengono definite solo se la base è positiva. Se così nn si facesse sorgerebbero alcune antinomie. Ad esempio consideriamo (−2)3 come potenza a esponente razionale.
Non potendo essere usati come base per le potenze i numeri negativi non sono utilizzabili nemmeno come basi dei logaritmi.
È facile osservare che il logaritmo in base a di un numero x è la funzione inversa dell’elevamento a potenza ax, pertanto, a partire dalle proprietà delle potenze è possibile ricavare analoghe proprietà per i logaritmi.
PROPRIETA’ DEI LOGARITMI
- Il logaritmo del prodotto di due numeri è uguale alla somma dei logaritmi dei singoli numeri:
loga( b1 * b2) = loga(b1) + loga(b2)
- Il logaritmo del quoziente di due numeri è uguale alla differenza dei logaritmi del numeratore e del denominatore:
loga( b1 / b2) = loga(b1) – loga(b2)
Dalla questa proprietà discende che il logaritmo del reciproco di un numero è uguale all’opposto del logaritmo del numero stesso:
loga( 1 / b) = loga(1) – loga(b) = – loga(b)
- Il logaritmo di una potenza bm è uguale all’esponente m (della potenza) moltiplicato il logaritmo della base y
(della potenza):
log(bm) = m*log (b)
Definizione
Assegnato il logaritmo di un numero positivo x rispetto ad una base a>1, è possibile determinare il logaritmo dello stesso numero x rispetto ad una diversa base b>1 come segue:
IN SINTESI:

NE DERIVANO:
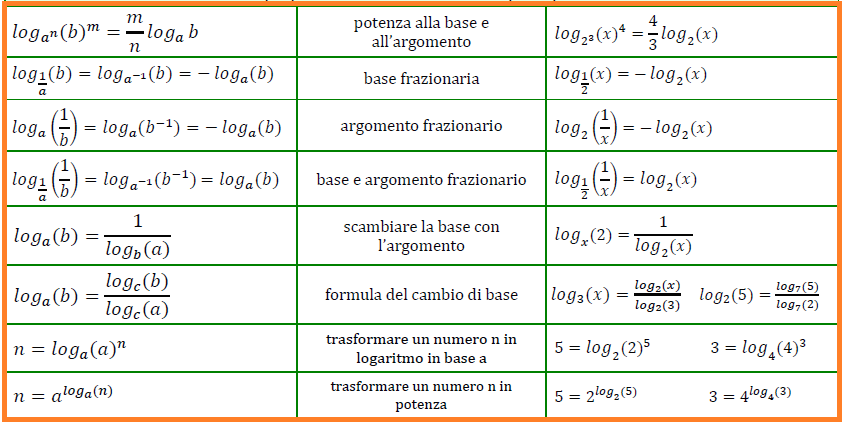
LA FUNZIONE LOGARITMICA
DEFINIZIONE
Si chiama funzione logaritmica ogni funzione del tipo:
y = loga x, con a > 0 e a <> 1.
Poiché l’argomento del logaritmo deve essere positivo, il dominio della funzione è :R+; si dimostra che la funzione assume tutti i valori reali, quindi il codominio è R.
Fissata la base a, la funzione logaritmica è così definita:
f: R+=>R, f: x => y = loga x.
Studiamo il grafico della funzione y = loga x, nei due casi a > 1 e 0<a < 1.
Primo caso: a > 1
Scegliamo, per esempio, a = 2, e studiamo la funzione y = log2 x.
Compiliamo una tabella, attribuendo a x valori positivi.
Disegniamo nel piano cartesiano i punti ottenuti e, con l’aggiunta di altri punti,
otteniamo il grafico di y = log2 x

Secondo caso: 0< a < 1
Scegliamo a = 1/2,
quindi la funzione è y = log1/2(x)
Compiliamo di nuovo una tabella e disegniamo il grafico.

I grafici di y= log2(x) e y = log1/2(x) sono simmetrici l’uno dell’altro rispetto all’asse x. Infatti, per la formula del cambiamento di base, si ha


Logaritmi decimali e logaritmi naturali
Tra tutti i logaritmi assumono particolare importanza quello in base 10
, che viene comunemente chiamato logaritmo decimale o di Briggs (e si indica con log), e quello in base e, che viene comunemente detto logaritmo naturale o di Nepero e si indica con ln . e è un numero irrazionale che ha il seguente valore approssimato:
Le tavole logaritmiche che forniscono i logaritmi in base 10 sono comunque utilizzabili anche per il calcolo di logaritmi in base e (come del resto di logaritmi in qualsiasi base); infatti, per la proprietà relativa al cambiamento di base, il logaritmo in base e di un qualsiasi numero x positivo è:
ln x=log x\log e
(3751)
