
Risolvere l’equazione goniometrica
19sen x + 3cos x − 9 = 0
e scrivere esplicitamente le soluzioni che cadono in [0 , 2π].
SOLUZIONE
I METODO
Si tratta di un’equazione lineare in seno e coseno, che può essere risolta ad esempio tramite l’applicazione delle note formule razionali in
tg x/2.
Abbiamo infatti:
Le formule parametriche
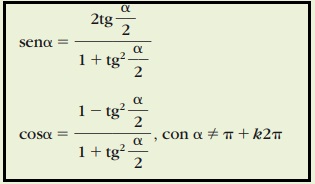

da cui 6t2− 19t + 3 = 0, se poniamo tg x/2 = t .
Ora, le soluzioni di questa equazione di secondo grado sono
t1 = 1/6 e t2 = 3
Per trovare x potremmo utilizzare la funzione arcotangente,
ma possiamo anche ragionare come segue:
se tg x/2 = 1/6 possiamo facilmente trovare sen x e cos x applicando ancora le formule razionali in tg x/2;
otteniamo infatti:

il che significa che x giace nel primo quadrante: esso può essere espresso indifferentemente come
x = arcsen 12/37 oppure x = arccos 35/37
Applicando lo stesso procedimento al caso tg x/2 = 3 otteniamo invece
sen x = 3/5 e cos x = -4/5
ora, l’angolo α che ha tali funzioni goniometriche non può essere espresso come x = arcsen 3/5 perché α giace nel primo quadrante, mentre l’angolo che stiamo cercando giace nel secondo.
Il problema si risolve semplicemente considerando l’angolo arccos (-4/5);
perciò tutte le soluzioni dell’equazione sono:

II METODO
Esiste anche un altro procedimento per la risoluzione di equazioni lineari in seno e coseno, che consiste nell’interpretazione grafica dell’equazione, o meglio di un sistema ad essa equivalente.
Riprendiamo ancora la stessa equazione lineare;
se poniamo senx = Y e cosx = X (il che si giustifica ricordando la definizione delle funzioni seno e coseno), l’equazione diventa
19Y + 3X − 9 = 0
che è in due variabili.
Basta però ricordare la relazione fondamentale della goniometria, grazie alla quale è sempre
X2+ Y2= 1
in conclusione, l’equazione data è equivalente al sistema

che dal punto di vista della geometria analitica non è altro che l’intersezione tra una retta ed una circonferenza. Ovviamente, possiamo osservare che troviamo le stesse soluzioni di prima.
Il vantaggio di questo procedimento sta non solo nel fatto che otteniamo direttamente seno e coseno degli angoli in questione senza passare per la tangente di x/2, ma anche nel fatto che in questo modo determiniamo anche le soluzioni che potrebbero sfuggire applicando le formule razionali ricordate sopra.
Esempio
Si consideri infatti ad esempio l’equazione
7sen x − 4cos x − 4 = 0
Applicando le formule in tg x/2 troviamo:

Tuttavia, in questo modo, non esauriamo tutte le soluzioni dell’equazione data.
In effetti, occorre ricordare che le formule in tg x/2 non sono valide per x = π (più in generale, non sono valide nei multipli dispari dell’angolo piatto), perché tg x/2 non esiste.
La soluzione “mancante” (perché il grado dell’equazione è solo 1 anziché 2) è proprio π, perciò alle soluzioni trovate prima dobbiamo aggiungere x = π + 2kπ.
Ora, applicando il secondo procedimento, il problema non si pone, perché il punto (−1 ; 0) è un punto come un altro, e non va trattato a parte.
In effetti, il sistema

che corrispondono alle soluzioni trovate prima.
(147)
