La funzione arcocoseno

Definizione

Dato un qualunque numero x compreso tra −1 ed 1 (estremi inclusi), si dice arcocoseno del numero x (e si indica con arccos x),l’unico angolo  α compreso tra 0 e π tale che cos α è uguale ad x.
Perciò abbiamo arccos x = α se cos α = x, ma con la limitazione 0 ≤ α ≤ π.

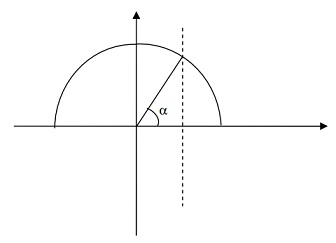
Anche qui possiamo dare un’interpretazione geometrica:

per determinare l’arcocoseno di un numero a, consideriamo l’unica intersezione tra la retta di equazione x = a e la semicirconferenza goniometrica giacente nel semipiano delle ordinate non negative. Se a è positivo l’intersezione cade nel primo quadrante, ed in tal caso
arccos  a è un angolo acuto; se invece a è negativo l’intersezione cade nel secondo quadrante, ed in tal caso arccos a è un angolo ottuso.

Perciò abbiamo i seguenti risultati:

mentre ad esempio scritture come arccos 1 = 2π o arccos(−1) = −π sono errate, in quanto gli angoli trovati non cadono tra 0 e 2π.

La figura seguente mostra il grafico della funzione arcocoseno:

Si osservi anche che, a differenza di quanto accade per l’arcoseno, ad argomento minore corrisponde risultato maggiore: la funzione arcocoseno assume il suo valore minimo (che è 0) per x = 1, ma per x minore di 1 assume valori via via maggiori, fino a raggiungere il suo massimo (cioè π) per x = −1.
Un’altra importante differenza tra arcoseno e arcocoseno è che quest’ultima funzione non è né pari né dispari: di conseguenza, un’espressione come arccos(−a) non può essere scritta in modo più semplice.

Le soluzioni dell’equazione cos x = a

Vediamo allora come si esprimono le soluzioni dell’equazione cos x = a.

Consideriamo ad esempio l’equazione cos x = 8/9:

tutte le soluzioni si possono esprimere tramite la formula:

partendo come al solito dal punto A = (1 ; 0) e percorrendo la circonferenza goniometrica in senso antiorario, troviamo

Riassumendo, per a ∈ (−1 , 1), le soluzioni dell’equazione cos x = a sono:

x ±arccos a + 2kπ

Esempio

Risolvere l’equazione goniometrica 6sen x cos x − 2sen x + 9cos x − 3 = 0, e scrivere esplicitamente le soluzioni che cadono in [0 , 2π].

SOLUZIONE

Mediante un semplice raccoglimento parziale, l’equazione si trasforma in

(2 sen x + 3)(3 cos x − 1) = 0

da cui senx = −3/2 oppure cos x = 1/3.

La prima equazione ovviamente non ha soluzioni reali, mentre dalla seconda abbiamo

(588)