
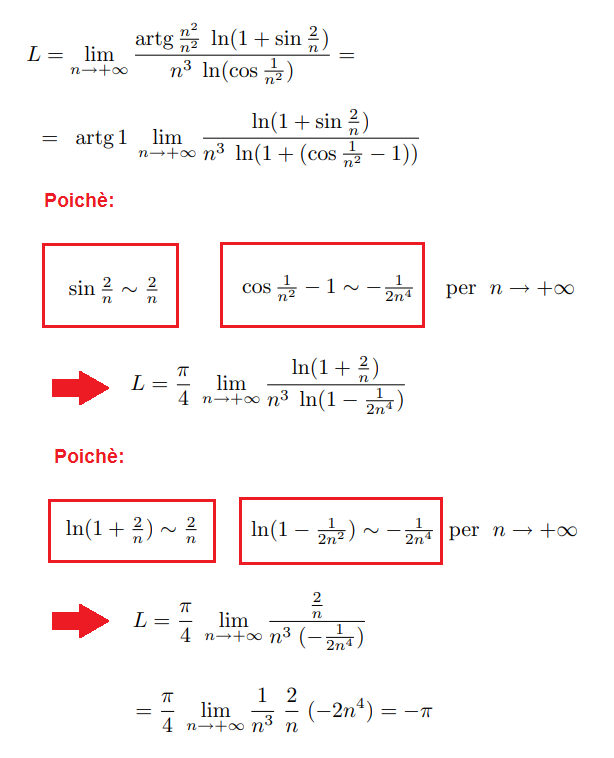
ESERCIZIO 1
Calcolare il limite

SOLUZIONE
Per la gerarchia degli infiniti, si ha
ESERCIZIO 2
Stabilire se le funzioni f e g , definite da
per x ≥ 0 , sono asintoticamente equivalenti per x → +∞.
SOLUZIONE
Si tratta di calcolare il limite

Per la gerarchia degli infiniti, si ha

Pertanto, le due funzioni f e g non sono asintoticamente equivalenti per x → +∞.
Ricordiamo che due funzioni sono asintoticamente equivalenti se il limite del loro rapporto è 1….
ESERCIZIO 3
Si consideri la funzione f : R → R definita, per ogni x ∈ R , da

(a) Verificare che la funzione f è effettivamente definita su tutto R .
(b) Determinare gli eventuali asintoti di f .
(c) Calcolare la derivata prima di f .
(d) Determinare i punti di massimo e di minimo di f .
(e) Disegnare il grafico qualitativo di f .
(f) Senza calcolare la derivata seconda di f , determinare il numero minimo di punti di flesso di f .
(g) Determinare l’immagine I di f .
(h) Determinare i punti in cui f è localmente invertibile.
(i) Scrivere lo sviluppo di Taylor del secondo ordine nel punto x0 = 1 , con resto secondo Peano, della funzione g definita da

SOLUZIONE
Si consideri la funzione f : R → R definita, per ogni x ∈ R , da

(a) Poichè ex > x per ogni x ∈ R , si ha che f è effettivamente definita su tutto R.
(b) Poichè si ha

→ la funzione f ammette la retta di equazione y = 0 come asintoto orizzontale per x → +∞ ed ammette la retta di equazione y = −1 come asintoto orizzontale per x → −∞ .
(c) La derivata prima di f è

(d) Si ha f’ (x) ≥ 0 se e solo se x ≤ 1 . Pertanto, la funzione f ha un punto di massimo in x = 1 . Più precisamente, ha un punto di massimo in 
(e) Il grafico di f è

(f) La funzione f possiede almeno due punti di flesso.
(g) L’immagine di f è l’intervallo

(h) La funzione f è localmente invertibile per ogni x ≠ 1 .
Funzioni localmente invertibili
Per funzioni f : R → R derivabili, la condizione f′ > 0 (o f′ < 0) è sufficiente a garantire la monotonia e quindi l’ invertibilità di f e la derivabilità della funzione inversa. Inoltre per funzioni con derivata continua l’essere f′(x0) ≠ 0 in un punto x0, assicura l’esistenza di un intervallo I(x0, r) su cui f′(x) ha lo stesso segno di f′(x0), da cui la stretta monotonia, la continuità, la derivabilità di (f|I )−1 e la formula
Definizione.
Una funzione f : Ω ⊂ R → R si dice localmente invertibile se per ogni x ∈ Ω esiste un intorno U di x tale che f|U è iniettiva.
(i) Lo sviluppo di Taylor del secondo ordine nel punto x0 = 1 , con resto secondo Peano, della funzione g è:

Formula di Taylor
Definizione
Sia f : (a, b) -> R derivabile n volte in x0 ∈ (a, b). Allora la scrittura
e nota come formula di Taylor di ordine n, centrata in x0, con resto di Peano.
Inoltre
si chiama polinomio di Taylor.
ESERCIZIO 4
Per x → 0 , determinare la parte principale della funzione

SOLUZIONE
Per x → 0 , si ha

Pertanto, la parte principale di f(x) , per x → 0 , è 3x3
[elementor-template id=”10963″]
[elementor-template id=”10428″]
(343)



