Le Equazioni Differenziali

Di norma, per ottenere un integrale (o soluzione) particolare di un’equazione differenziale, della quale si sa calcolare l’integrale generale:

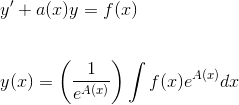
– se l’equazione è del 1° ordine basta una condizione;
– se l’equazione è del 2° ordine occorrono due condizioni.

Infatti, in quest’ultimo caso, come vedremo fra breve attraverso un esempio, intervengono due parametri effettivi nell’integrale generale.
Ciascuna di tali condizioni si chiama condizione iniziale.

Si consideri un’equazione differenziale del 1° ordine, che nella sua forma generica è scritta nel modo seguente: F(x, y(x), y'(x))=0. Il problema consistente nella ricerca di un suo integrale particolare sotto la condizione y(x₀)=y₀, detta condizione iniziale, dove x₀ ed y₀ sono valori reali assegnati , è quello che si denomina un particolare problema di Cauchy.

Per esempio, è un “problema di Cauchy” quello di risolvere l’equazione differenziale y’(x)=x sotto la condizione y(0)=1. Esso ammette una ed una sola soluzione, la funzione:

Naturalmente se si sa calcolare l’integrale generale di un’equazione differenziale, la ricerca di un integrale particolare, e quindi la risoluzione del relativo problema di Cauchy, è un’operazione del tutto banale. A volte tuttavia si riesce a risolvere il problema di Cauchy senza conoscere l’integrale generale dell’equazione differenziale.
Ora però, l’integrazione delle equazioni differenziali ed in particolare la risoluzione di un problema di Cauchy sono operazioni assai complesse che, peraltro, solo in situazioni davvero eccezionali si concludono con esito positivo, nel senso cioè che viene trovata una soluzione. A parte il fatto che un problema di Cauchy non sempre ammette soluzione e, quando l’ammette, non è detto che sia unica.
In ogni caso, fra tali situazioni eccezionali noi ne prenderemo in esame solo alcune assolutamente elementari e nelle quali comunque si riesce a determinare l’integrale generale dell’equazione, rinviando a studi universitari la risoluzione di un vero e proprio problema di Cauchy.

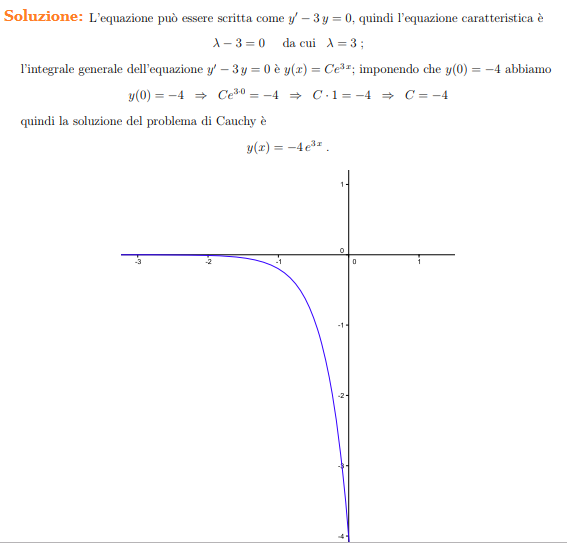
Risolvere il seguente problema di Cauchy:

 LE EQUAZIONI DIFFERENZIALI DEL TIPO y’= f(x)

METODO

Per risolvere un’equazione differenziale del primo ordine, riconducibile al tipo

y’ = f (x)

– si isola y’ ;
– si integrano entrambi i membri:

ricordando che:

– si calcola l’integrale indefinito di f (x);
le primitive di f (x) sono le soluzioni.

[inbound_button font_size=”20″ color=”#ff8040″ text_color=”#ffffff” icon=”” url=”https://matematicaoltre.altervista.org/le-equazioni-differenziali-2/” width=”” target=”_self”]Equazioni differenziali a variabili separabili[/inbound_button]

(78)