Che cos’`e l’interpolazione?

Che cos’`e l’interpolazione?

Spesso, in diversi campi scientifici, si deve affrontare il problema di interpretare, valutare e gestire dati ricavati da rilevazioni statistiche o da esperimenti riguardanti un fenomeno. Il problema è piuttosto complesso, mentre noi vogliamo soltanto dare un’idea di come si può affrontarlo e ci limitiamo a casi semplici.

Studiamo problemi che riguardano relazioni fra due sole variabili x e y, delle quali conosciamo alcune coppie di valori (x_i, y_i), rilevati da un’indagine
statistica e che vogliamo interpretare tramite una funzione y = f (x).

Consideriamo quindi le coppie ordinate di valori (x_i, y_i) e rappresentiamole in un piano cartesiano tramite punti, ottenendo quello che chiamiamo diagramma a dispersione o nuvola di punti.

Vogliamo determinare una funzione matematica, che chiameremo funzione interpolante, in grado di rappresentare il fenomeno studiato.

Vogliamo determinare una funzione matematica, che chiameremo funzione interpolante, in grado di rappresentare il fenomeno studiato.

1 Se la funzione assume esattamente i valori rilevati, e quindi il suo grafico passa per tutti i punti del diagramma a dispersione, parliamo di interpolazione per punti noti o interpolazione matematica;

Vogliamo determinare una funzione matematica, che chiameremo funzione interpolante, in grado di rappresentare il fenomeno studiato.

2 Se la funzione assume valori vicini ai valori rilevati e quindi il suo grafico passa fra i punti del diagramma a dispersione, parliamo di interpolazione fra punti noti o interpolazione statistica.

ESEMPIO:

Supponiamo di avere un insieme di valori della quantità y corrispondenti a valori della quantità x, ad esempio, la seguente sequenza di valori x_i, y_i che plottiamo in un grafico.

 

Dal grafico, sospettiamo che esista una relazione lineare tra x e y:

y = mx + q.

Effettivamente i punti possono essere congiunti abbastanza facilmente con una retta. La pendenza e l’intercetta possono essere misurate e, in particolare, usando il primo e l’ultimo dei punti plottati, si trova che la pendenza della retta è 3/8 mentre l’intercetta è 2.

Da un’analisi più attenta del grafico si intuisce che alcuni punti (x_i, y_i) non appartengono alla retta. Verifichiamo ciò calcolando i residui o errori di accostamento r_i = y_i − mx_i − q:

Il grafico tracciato appare però soddisfacente, poichè tutti i punti risultano quasi sulla retta.

Interpolazione statistica: il caso lineare

Più spesso, tuttavia, specialmente quando si ha a che fare con dati sperimentali, dall’analisi dei grafici si ha una forte impressione che una relazione lineare debba esistere, ma è veramente difficile determinare ad occhio la posizione della retta.

Consideriamo ad esempio il seguente set di punti:

che plottiamo nel grafico seguente

L’impressione `e che i dati si dispongano intorno ad una retta, ma la posizione esatta della retta diventa una questione di gusto personale

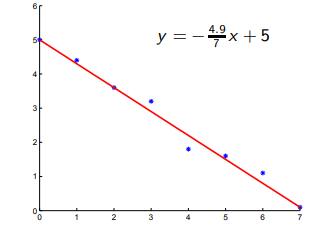
1 Come prima, infatti, possiamo tracciare la retta passante per il primo e l’ultimo dei punti, di equazione y = (−4.9/7)*x + 5 e giudicarla adeguata

Qualcuno potrebbe giudicare la retta di equazione

che lascia sopra e sotto di se un numero uguale di punti più adeguata

Qualcun’altro potrebbe decidere che i punti più al centro sono più importanti e pertanto giudicare migliore la rappresentazione fornita dalla retta di equazione

Come determinare la retta y = mx + q?

I residui.

Se il punto (x_i, y_i) giace sulla retta y = mx + q, allora risulta

r_i = y_i − mx_i − q = 0;

d’altro canto, se il punto (x_i, y_i) è esterno alla retta y = mx + q, allora risulta

r_i = y_i − mx_i − q ≠ 0.

Il residuo r_i rappresenta la distanza (con segno) tra il dato (x_i, y_i) e il punto sulla retta (x_i, mx_i + q) corrispondente al valore x_i della variabile. Il residuo r_i ha valore positivo o negativo dipendentemente dal fatto che il punto plottato giace sopra o sotto la retta.

Non potendo annullare tutti i residui (ciò capita solo se i punti sono allineati, e y = mx + q è esattamente la retta passante per essi) possiamo pensare di annullare la loro somma:

La precedente equazione può anche essere scritta nel seguente modo

Il numero r e detto residuo totale. 

La sola equazione (1) nelle incognite m e q non è sufficiente a determinare in modo univoco una retta y = mx + q. Inoltre il residuo totale può essere nullo anche nel caso in cui la retta y = mx + q non si adatta affatto ai dati!

Un esempio chiarificatore.

Consideriamo il seguente set di dati

non è difficile verificare che ogni retta di equazione y − 4 = m (x − 4) è tale che

con residui che tendono ad infinito per m tendente ad infinito.

Il metodo delle medie

Naturalmente non riusciamo a determinare i valori di m e q dall’equazione (1) poichè essa contiene due incognite. Però possiamo dividere i punti dati in due gruppi e costituire due equazioni separate della forma (1). Detti quindi I₁, I₂ due insiemi non vuoti di indici tali che:

consideriamo il sistema di due equazioni in due incognite:

dove con n₁ e n₂ abbiamo denotato rispettivamente le cardinalità (numero di elementi di) di I₁ e I₂ . Le due equazioni ci consentiranno di calcolare i valori di m e di q. Come si vede il metodo delle medie non presenta alcuna difficoltà di calcolo; è inoltre possibile mostrare che questo metodo può produrre soluzioni sorprendentemente buone, a patto che il raggruppamento delle equazioni è realizzato in modo appropriato.

Applichiamo la procedura al secondo set di dati presentati.

Poniamo le due equazioni a sistema:

 

 

 

 

 

 

 

LEGGI: IL METODO DEI MINIMI QUADRATI

Torna alla pagina di Statistica:

Statistica

 

(765)