Esercizi svolti sui limiti di funzione

Breve ripasso:

Definizione di o piccolo

Dalla definizione abbiamo subito:

come nel seguente esempio:

Per il calcolo di limiti che si presentano nelle forme indeterminate del tipo 0/0 o ∞/∞ faremo uso anche dei seguenti risultati.

TEOREMA DI DE L’HOPITAL

TEOREMA DI DE L’HOPITAL – ALCUNI ESEMPI

Indicheremo, inoltre, nel corso degli esercizi con (H) l’applicazione del teorema di De L’Hopital.

E spesso utile tenere a mente alcuni “limiti notevoli”, tra i quali ricordiamo:

Limiti notevoli

QUI TROVI TUTTI I LIMITI NOTEVOLI

Sarà  di estrema utilità nel calcolo dei limiti la formula di Taylor (con il resto di Peano):

valida per esempio per funzioni derivabili n + 1 volte in un intorno di a.Il polinomio di Taylor di f di ordine n e di centro a verrà indicato con

Dalla formula di Taylor e dalla definizione di “o piccolo” si ottiene subito che in certi limiti si può sostituire alla funzione il suo polinomio di Taylor, dall’uguaglianza

QUI TROVI TUTTO SUGLI SVILUPPI DI TAYLOR

Formule di MacLaurin più usate (h, n numeri interi non negativi; a numero reale):

ricordiamo che:

Quello di Taylor  è uno sviluppo che approssima una funzione definita in un intervallo aperto ( x₀−δ,x₀+δ) , centrato quindi in un punto x₀ .

Lo sviluppo di McLaurin approssima invece la funzione nell’origine, dunque nel punto x₀=0 .

 

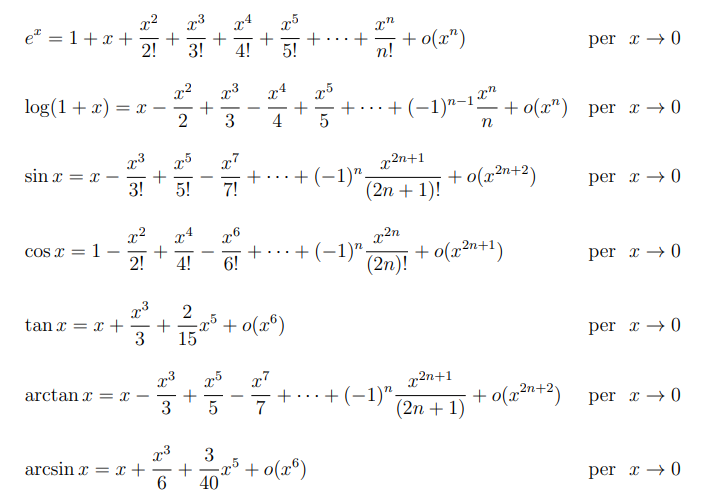
ESERCIZIO 1: 

Calcolare:

a)

b)

SOLUZIONE:

Cercheremo di svolgere questo esercizio usando per quanto possibile la regola di De l’Hospital. Verifichiamo prima di tutto che si tratti di una forma indeterminata.

a)

b)

 

ESERCIZIO 2: 

Calcolare il seguente limite:

SOLUZIONE:

Il limite si presenta nella forma indeterminata ∞⁰:

Calcoliamo il logaritmo del limite:

Abbiamo quindi ricondotto la forma indeterminata ∞⁰ alla forma indeterminata ∞/∞.

Possiamo perciò applicare la regola di De L’Hospital:

ESERCIZIO 3: 

Calcolare i seguenti limiti, prima utilizzando le formule di MacLaurin opportunamente arrestate e successivamente usando il teorema di de l’Hospital:

SOLUZIONE:

a)

b)

c)

ESERCIZIO 4: 

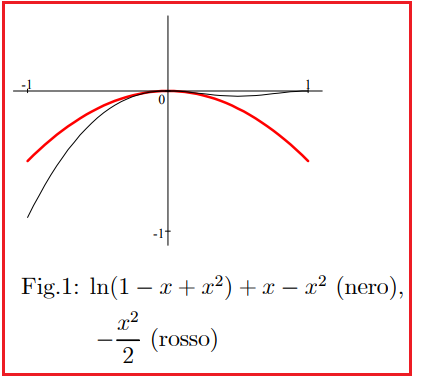
È vero che, per x che tende a 0, la funzione

ln(1 − x + x²) + x − x² è o(x²)?

Motivare l’affermazione.

SOLUZIONE:

Per x che tende a 0, la funzione ln(1 − x + x²) + x − x² NON è o(x²).
Infatti sostituendo t = x−x² nella formula di MacLaurin di ln(1 + t) arrestata al second’ordine:

[elementor-template id=”10963″]

 

(387)