
LA DISTRIBUZIONE BINOMIALE (O DI BERNOULLI)
Molti degli esempi che abbiamo presentato negli articoli precedenti possono essere pensati come casi particolari di uno schema generale di prove ripetute, ad esempio successivi lanci di un dado, di una moneta, estrazioni di palline da un’urna, di carte da un mazzo (in questi ultimi due casi reimmettendo la pallina o la carta nell’ urna o nel mazzo), estrazioni di numeri del lotto in settimane successive, e così via.
Lo schema generale può essere descritto mediante la seguente definizione:
COS’E’ LA DISTRIBUZIONE BINOMIALE
Si dice esperimento di Bernoulli una sequenza di n prove con le seguenti caratteristiche:
1) il risultato di ogni prova può essere solo “successo” o “fallimento”;
2) il risultato di ciascuna prova è indipendente dai risultati delle prove precedenti;
3) la probabilità p di “successo”, e quindi la probabilità q = 1 – p di “fallimento”, sono costanti in ciascuna prova.
Ci proponiamo ora di determinare la probabilità che, in n prove di un esperimento di Bernoulli, si abbiano esattamente k successi.
Indichiamo con S il successo e con F il fallimento. Una sequenza di n prove darà, per la 1), come esito una sequenza di n fra S e F.
Ad esempio, una sequenza che contiene k successi è la seguente:

Se p è la probabilità di S e q la probabilità di F, la probabilità di ottenere proprio quella sequenza è, trattandosi di eventi indipendenti e applicando la regola della probabilità composta:

È immediato convincersi che una qualsiasi altra sequenza contenente esattamente k successi avrà sempre come probabilità
pk⋅ qn–k (cambia l’ordine dei fattori, ma non il prodotto).
Per determinare in quanti modi si possono ottenere k successi in n prove, basta scegliere tra gli n numeri 1, 2, …, n i k che contrassegnano i posti occupati dai successi: ciò può essere eseguito in C modi (non essendo rilevante l’ordine in cui tali posti vengono scelti).
In definitiva si hanno Cn,k possibilità di ottenere k successi in n prove e ciascuna di esse ha, come si è detto, probabilità pk* q n–k. Dato che queste possibilità distinte corrispondono al realizzarsi di eventi incompatibili (evidentemente il realizzarsi di una certa sequenza di S e F è incompatibile con il verificarsi di un’altra di tali sequenze), per la regola delle probabilità totali, la probabilità cercata, che indichiamo con pn(k) , è:

o, usando la notazione dei coefficienti binomiali:

Esempio 1.
Determinare la probabilità che su 12 lanci di una moneta buona si ottengano esattamente 8 teste.
Si tratta di un esperimento di Bernoulli in cui il “successo” coincide con “esce T”; quindi p =q =1/2 e si ha:

Esempio 2.
Determinare la probabilità che estraendo per 5 volte una carta da un mazzo da 40 (inserendo ogni volta la carta estratta e rimescolando bene il mazzo) si ottengano:
a) esattamente 3 figure
b) almeno 3 figure
c) almeno una figura
Si osservi che, se non si reintroducesse la carta nel mazzo, l’esperimento non sarebbe di Bernoulli, in quanto la probabilità di estrarre una figura cambierebbe ad ogni successiva estrazione. In questo caso, invece, si tratta di un esperimento di Bernoulli in cui il “successo” è l’estrazione di una figura, per cui

a) La probabilità di ottenere esattamente 3 figure è:
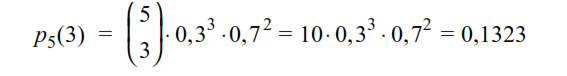
b) La probabilità di ottenere almeno 3 figure è la somma delle probabilità di ottenere esattamente 3, 4 o 5 figure:
![]()
c) Per rispondere a quest’ultima domanda si può procedere come in b) calcolando:
![]()
È tuttavia molto più rapido considerare la probabilità dell’evento contrario, ossia la probabilità di non ottenere alcuna figura:

per cui la probabilità di ottenere almeno una figura è:
1 – 0,16807 = 0,83193.
Esempio 3.
Un’urna contiene 10 palline di cui 3 bianche. Si eseguono 4 successive estrazioni rimettendo ogni volta la pallina estratta nell’urna. Determinare la distribuzione di probabilità della variabile casuale X = “numero di palline bianche estratte” e rappresentarla con un istogramma.
La probabilità di estrarre una pallina bianca è 0,3. La variabile casuale X ha come possibili valori 0, 1, 2, 3 e 4 e le rispettive probabilità sono:
![]()
Determiniamo tali valori ricorrendo alla Tavola:

L’istogramma risulta:
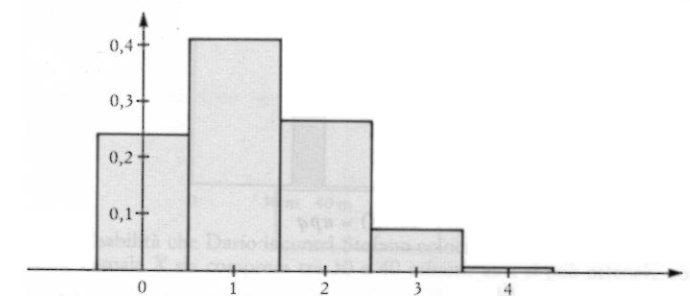
Esempio 4.
Rappresentare con un istogramma la distribuzione binomiale con n = 10 e p = 0,9.
Per sfruttare la Tavola anche in questo caso, occorre osservare che avere probabilità 0,9 di successo equivale ad avere probabilità 0,1 di insuccesso. Quindi, ottenere 3 successi in 10 prove equivale ad ottenere 7 insuccessi, per cui p10 (3) con p = 0,9 si può leggere in corrispondenza di p10(7) con p = 0,1, e così via:

(dove compare 0,0000 non si intende evidentemente probabilità nulla, ma un valore molto basso, inferiore a 0,00005). L’istogramma è il seguente:

Per una variabile casuale con distribuzione binomiale si può dimostrare che:
il valore medio è: E(X) = np
la varianza vale: var(X) = npq
CONTINUA A LEGGERE: CARATTERISTICHE DELLA DISTRIBUZIONE BINOMIALE E LA DISTRIBUZIONE NORMALE
(503)
