
Esempi tipici di questa situazione sono i seguenti.
1 Il sondaggio di opinione: si vuole stimare la proporzione p della popolazione complessiva che è daccordo con una certa opinione, osservando il valore che questa proporzione ha su un campione di n individui.
2 La produzione di un dato tipo di oggetto: il produttore vuole poter garantire che la proporzione di pezzi difettosi in una data produzione non superi un certo valore prefissato; occorre quindi determinare, esaminando un campione, un intervallo di confidenza per la proporzione p di pezzi difettosi in una produzione, ed eventualmente intervenire sulla produzione affinché la proporzione di pezzi difettosi non superi una certa soglia fissata.
3 Lo studio della diffusione di una data malattia: si vuole stimare qual è la proporzione di pazienti di una certa popolazione che ha una data malattia, studiando il valore di questa proporzione su un campione di n persone appartenenti a quella popolazione.
Per stimare la proporzione di una popolazione procediamo nello stesso modo in cui abbiamo stimato la media di una popolazione.
Ad esempio, consideriamo se un consumatore scelto a caso preferisce il nostro prodotto o quello della concorrenza. Siamo interessati alla proporzione nella popolazione, indicata con π, che viene stimata dalla proporzione campionaria, indicata con p.
Proporzione campionaria

La proporzione assume valori compresi tra 0 ed 1, estremi inclusi.
La proporzione campionaria è uno stimatore non distorto della proporzione nella popolazione (così come la media campionaria è uno stimatore non distorto per la media della popolazione).
Errore standard della proporzione campionaria
L’errore standard della proporzione campionaria, misura la dispersione delle proporzioni campionarie (osservate in tutti i possibili campioni) attorno alla proporzione della popolazione:

Se consideriamo tutti i possibili campioni di una certa ampiezza, la distribuzione di tutte proporzioni campionarie si dice distribuzione campionaria della proporzione.
Quando il campionamento è effettuato con reimmissione (da una popolazione di ampiezza finita), la distribuzione della proporzione è legata alla binomiale.
Quando nπ e n(1 −π) sono entrambi almeno uguali a 5, la distribuzione binomiale puòessere approssimata con la distribuzione normale. Quindi per valutare alcune probabilità relative alla proporzione campionaria, possiamo standardizzare ed utilizzare la distribuzione normale:
Standardizzazione della proporzione campionaria
In altri termini la statistica:

ha approssimativamente la distribuzione normale standardizzata per grandi valori di n.
Quindi quando n è grande si può costruire un intervallo di confidenza per il parametro p, usando lapprossimazione normale per la distribuzione binomiale.
Possiamo affermare che

ossia, con probabilità 1 – α, vale la disuguaglianza

Per ricavare lintervallo di confidenza per π occorrerebbe risolvere la disuguaglianza (2) rispetto a π; questo non è difficile, ma il calcolo può essere notevolmente semplificato sostituendo nellespressione che compare al denominatore, la quantità π con la proporzione campionaria (1) (facendo questa sostituzione si ottiene in effetti un intervallo di confidenza approssimato).
In questo modo,in generale, estraendo un campione di ampiezza n da una popolazione bernoulliana e indicando con pˆ la proporzione del campione, si ottiene il seguente intervallo di confidenza per la proporzione p della popolazione bernoulliana, con grado di fiducia (1-α) * 100% valido per grandi campioni.

Il valore critico z α/2 viene scelto con la stessa regola già indicata per lintervallo di confidenza per la media, nel caso dei grandi campioni.
Per verificare le condizioni di applicabilità dellapprossimazione della binomiale con la normale, ossia

questa verifica si può fare solo dopo aver effettuato il campionamento: se le condizioni precedenti non sono soddisfatte, il risultato è privo di valore, e occorre ripetere il campionamento aumentando lampiezza n del campione.
Esempio
In un campione di 400 persone a cui è stato somministrato un dato vaccino, 136 di esse hanno avuto effetti collaterali di un certo rilievo. Determinare un intervallo di confidenza con grado di fiducia del 95% per la proporzione della popolazione che soffre di tali effetti collaterali.
Nel campione di n = 400 persone la proporzione campionaria è

e con la formula (3) si trova lintervallo di confidenza

Osserviamo che le condizioni per poter usare lapprossimazione della binomiale con la normale sono verificate, essendo

Esempio
Un campione di 100 votanti scelto a caso fra tutti i votanti di una regione ha indicato che il 55% di essi è favorevole ad un certo candidato.
a) Determinare gli intervalli di confidenza con grado di fiducia del 95% e del 99% per la proporzione di tutti i votanti a favore del candidato.
b) Confrontare queste stime con la stima che si trova se si usa un campione di 2000 votanti, con la stessa percentuale campionaria di favorevoli.
a) Per il grado di fiducia del 95% il valore critico è zα/2 = 1.96 ; il risultato campionario indica che ˆp = 0.55; l’intervallo di confidenza è:

Possiamo asserire con grado di fiducia del 95% che il candidato avrà a suo favore una percentuale di votanti compresa fra il 45% e il 65%.
Per il grado di fiducia del 99% il valore critico è zα/2 = 2.576; lintervallo di confidenza

Possiamo in questo caso asserire con grado di fiducia del 99% che il candidato avrà a suo favore una percentuale di votanti compresa fra il 42% e il 69%.
Lampiezza degli intervalli di confidenza trovati è troppo grande, ossia la precisione delle stime è troppo bassa.
b) Se il campione è di 2000 votanti, con il grado di fiducia del 95% si trova il seguente intervallo di confidenza:

In questo caso, con un grado di fiducia del 95%, il candidato avrà a suo favore una percentuale di votanti compresa fra il 52% e il 58%, con una stima decisamente più precisa. La maggior precisione dipende dalla maggiore ampiezza del campione.
Determinazione dell’ampiezza del campione per ottenere un errore prefissato
Con lo stesso procedimento già usato nel caso dell’intervallo di confidenza per la media di un grande campione, si può usare la disuguaglianza (3), valida con probabilità 1 – α, per ricavare una formula che consente di determinare lampiezza n del campione necessaria per ottenere un errore prefissato

Indicando con:

il massimo dellerrore che si commette approssimando la proporzione della popolazione p con la proporzione campionaria ˆP, la stima di E con probabilità 1 – α è data da
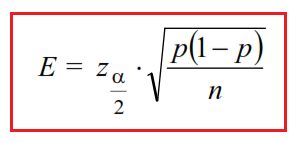
Dalla formula (4), risolvendo rispetto a n, si ricava lampiezza del campione necessaria per stimare la proporzione p con un errore prefissato E e con un dato grado di fiducia (si ricordi che n deve essere un intero):

Questa formula non può essere usata se non si ha qualche informazione sul valore di p; se tali informazioni non sono disponibili, si può far uso del fatto che il valore massimo che può assumere la quantità p(1-p) è 1/4, corrispondente a p = 1/2.
In questo caso lampiezza necessaria per il campione è (si ricordi che n deve essere un intero)

Per spiegarci meglio, facciamo questo
Esempio
Problema del sondaggio di opinione. Supponiamo che si voglia stimare la proporzione di elettori che approva l’operato del capo del governo; su un campione di 150 persone intervistate, 90 si sono dichiarate favorevoli.
Determinare un intervallo di confidenza con grado di fiducia del 95% per la proporzione degli elettori favorevoli al capo del governo e valutare la precisione della stima.
La proporzione campionaria dei favorevoli è

Lintervallo di confidenza con grado di fiducia del 95% è il seguente

La percentuale dei favorevoli, con un grado di fiducia del 95%, è compresa fra il 52% e il 68%: la stima è troppo imprecisa, l’ampiezza dell’intervallo è di 16 punti percentuali.
Può quindi essere utile determinare l’ampiezza del campione necessaria per ottenere una stima con precisione fissata. Stabiliamo ad esempio che si vuole una stima con una precisione dell’1% (corrispondente a un’ampiezza dell’intervallo non superiore a 2 punti percentuali), ossia fissiamo E = 0.01.
Dato che non abbiamo informazioni circa la percentuale dei favorevoli nel nuovo campione, dobbiamo usare la formula (5) e in tal caso, per il grado di fiducia del 95% , si ottiene

Esempio
Supponiamo di voler stimare la proporzione di pezzi difettosi in un lotto di oggetti di un dato tipo con un errore E = 0.04 e un grado di fiducia del 95% ; calcolare lampiezza necessaria per il campione, nel caso che
a) non si abbia alcuna informazione su quale possa essere la proporzione effettiva della popolazione;
b) si sappia che la proporzione della popolazione non supera il 12%.
a) Se non si ha alcuna informazione su p, si usa la formula (5), e con grado di fiducia del 95% si ricava

Occorre quindi un campione di ampiezza n = 601.
b) Se sappiamo che p ≤ 0.12 , con la formula (4.1) e con grado di fiducia del 95% si ottiene

Occorre in questo caso un campione di ampiezza n = 254.
Questo esempio illustra come il fatto di avere qualche informazione sul possibile valore della proporzione può sensibilmente ridurre la dimensione del campione.
[elementor-template id=”10808″]
[elementor-template id=”10688″]
(2734)
