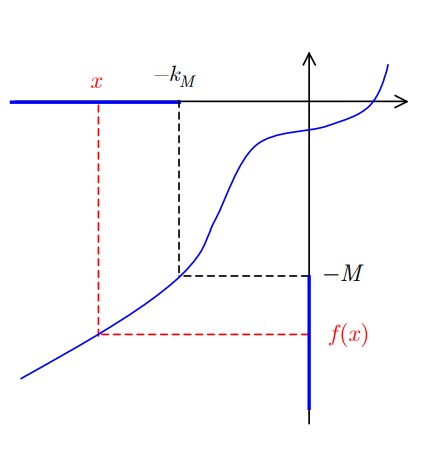
Limite infinito per x che tende all’infinito
Esprimiamo ora con rigore la crescita indefinita di una funzione verso valori positivi, quando la variabile indipendente tende verso valori positivi infinitamente grandi:
Definizione: Sia f x( ) una funzione con dominio illimitato superiormente; si dice che:


e quello di crescita indefinita verso valori positivi, quando la variabile indipendente tende verso valori negativi infinitamente grandi in valore assoluto:
Definizione: Sia f x( ) una funzione con dominio illimitato inferiormente; si dice che:


Analogamente si può esprimere con rigore la decrescita indefinita verso valori sempre più negativi, quando la variabile indipendente tende verso valori positivi infinitamente grandi:
Definizione: Sia f x( ) una funzione con dominio illimitato superiormente; si dice che:


e quello di decrescita indefinita verso valori sempre più negativi, quando la variabile indipendente tende verso valori negativi infinitamente grandi in valore assoluto:
Definizione: Sia f x( ) una funzione con dominio illimitato inferiormente; si dice che:


LEGGI ANCHE: Limite destro e sinistro in un punto
Esercizi svolti sui limiti
Esercizio 1
Verificare, ricorrendo alla definizione di limite, che

Soluzione
Prima di intraprendere la verifica del limite osserviamo che la funzione di cui si è calcolato il limite ha come dominio D l’insieme dei valori per i quali è soddisfatta la disequazione

Osserviamo inoltre che f(−1) = −1.
La verifica del limite consiste nel provare che per ogni ε > 0 esiste M > 0 tale che se x < −M allora

A questo punto sono necessarie alcune osservazioni
1. la verifica del limite avviene restringendo la funzione al sottoinsieme del dominio D∗ = D ∩ ℝ−= (−∞,−1] ossia, in termini pi`u semplici,
lavorando per x ≤ −1;
2. in D∗ la funzione è monotona strettamente decrescente. Infatti è composizione di funzioni monotone strettamente decrescenti in D;
3. in D∗ la funzione è limitata superiormente. Infatti per x ≤ −1 si ha

Dall’ ultima osservazione discende che la verifica del limite si riconduce allo studio della disequazione

Possiamo distinguere quindi due casi:
a) ε > 1/2: in questo caso per quanto osservato in 2. possiamo scegliere M = 1.
b) 0 < ε ≤ 1/2 nel qual caso la disequazione precedente si riconduce a

dove si è posto α=ε +1/2.
Possiamo risolvere la disequazione passando alla disequazione equivalente ottenuta elevando al quadrato membro a membro (ciascun membro è non negativo)

da cui M = α2/(2α − 1).
Esercizio 2
Calcolare il limite

Soluzione
Il limite si presenta inizialmente come una forma indeterminata del tipo [∞− ∞]. Per sciogliere la forma indeterminata possiamo in primo
luogo ricorrere al seguente artificio:

Utilizzando, tra le altre cose le proprietà dei radicali, possiamo riscrivere l’ultimo limite nella forma

Dal momento che stiamo calcolando il limite per x → −∞ possiamo porre ∣x∣ = −x e quindi il limite diviene

Esercizio 3
Calcolare il limite

Soluzione
Il limite si presenta nella forma indeterminata [∞/∞]. Per poterne calcolare il valore analizziamo separatamente numeratore e denominatore.
1. Numeratore. Il numeratore si presenta come una somma di due funzioni: la prima è un infinito per x → +∞ mentre la seconda è limitata:

2. Denominatore. Il denominatore si presenta come una somma di due funzioni che sono entrambe infinite per x → +∞. Per confrontare questi infiniti osserviamo che
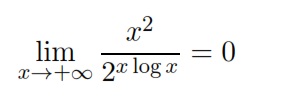
Ci`o segue direttamente dalle disuguaglianze

e dal teorema del confronto.
In conclusione raccogliendo a numeratore e a denominatore gli infiniti maggiormente rilevanti possiamo riscrivere il limite nella forma

Per concludere l’esercizio calcoliamo il limite del primo fattore

e 2x log 3 è un infinito per x →+∞.
GUARDA ALTRI ESERCIZI SUI LIMITI
(2305)
