
Le statistiche sulla sanità dicono che un americano su quattro soffre di qualche forma di malattia mentale. Pensa ai tuoi tre migliori amici. Se stanno bene, vuol dire che sei tu.”
RITA MAE BROWN
L’inferenza statistica (o statistica inferenziale) è il procedimento per cui si inducono le caratteristiche di una popolazione dall’ osservazione di una parte di essa (detta «campione”), selezionata solitamente mediante un esperimento casuale (aleatorio).
Nel caso finito dimensionale, ad esempio, da una popolazione di N individui, se ne estrae allora un sottoinsieme (campione) di n individui (n<N) da analizzare (campionamento).

• Spesso non è possibile misurare/osservare tutti gli elementi di una popolazione, ci si limita quindi allo studio di un campione e si stimano le caratteristiche della popolazione basandosi su quelle del campione.
Il reperimento dei DATI STATISTICI attraverso una RILEVAZIONE è un’operazione che ha dei COSTI, sia in termini di TEMPO IMPIEGATO che in termini ECONOMICI.
In molti ambiti scientifici, come in biologia e in medicina, si ha spesso a che fare con dati di origine sperimentale, per i quali quello di cui si dispone è sempre un campione, visto che la popolazione di riferimento è virtualmente “infinita” (es. un campione di animali da laboratorio rappresenta idealmente tutti gli esemplari di quella specie di animali da laboratorio).
• Con distribuzione campionaria di una statistica intendiamo una distribuzione di probabilità associata a tutti i possibili valori di quella statistica, calcolati per diversi campioni di taglia n.
– Campionamento casuale semplice di taglia n con rimpiazzo
Definizione
Si definisce Spazio dei Campioni l’insieme di tutti i possibili campioni di dimensione data (n) che possono essere estratti da una popolazione.
Nel caso descritto sopra la spazio campionario sarebbe costituito da tutte le possibili estrazioni con ripetizione di n elementi dagli N elementi della popolazione. Lo spazio dei campioni avrebbe cardinalità perciò Nn.
La statistica inferenziale ha il compito di fare inferenza sul campione cioè dall’analisi del campione deve dare dei criteri per «stimare» le caratteristiche che descrivono l’intera popolazione determinandone evidentemente la «bontà» e cioè, diciamo, il grado di coerenza.
In questo passaggio, poiché il campionamento è stato effettuato con criteri casuali, le “stime” che si ottengono sul campione, rispetto alla popolazione di partenza, sono per loro stessa natura affette da un errore, che si chiama errore di Campionamento.
Esempio
Se io calcolo la media delle altezze di un campione di persone, per le quali so che la popolazione di partenza ha media 175 cm, non otterrò mai esattamente una media pari a 175 cm.
Piuttosto, ripetendo infinite volte la stima su “infiniti” campioni, otterrò certamente una DISTRIBUZIONE DI MEDIE, che sarà dispersa attorno al vero valore della media, cioè 175 cm.
DISTRIBUZIONE NORMALE O DI GAUSS
E’ una distribuzione di probabilità di una variabile aleatoria continua caratterizzata da un grafico simmetrico «a forma di campana»
definizione:

Si dimostra che µ e σ sono rispettivamente il valor medio e lo scarto quadratico medio della variabile aleatoria X distribuita secondo la distribuzione normale.
Le caratteristiche più importanti della distribuzione normale sono le seguenti.
La funzione f(x) è definita su tutto l’asse reale e assume valori sempre positivi; è simmetrica rispetto alla retta
x = µ, cioè rispetto al valor medio della distribuzione. La moda e la mediana coincidono con il valor medio.
Il valore massimo della funzione viene assunto nel punto di ascissa µ ed è:
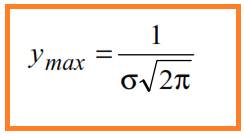 (*)
(*)
questo valore è perciò inversamente proporzionale a σ .
Lo scarto quadratico medio σ è uguale alla distanza dei punti di flesso da µ, ossia i punti di flesso hanno ascissa rispettivamente µ − σ e µ + σ .
E’ caratterizzata da un grafico simmetrico «a forma di campana»:
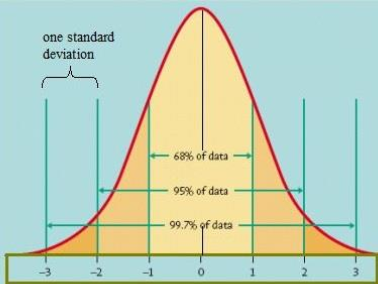
Poiché la curva rappresenta l’andamento della funzione di densità di una variabile aleatoria, il valore di tutta l’area sottesa da tale curva è uguale a 1.
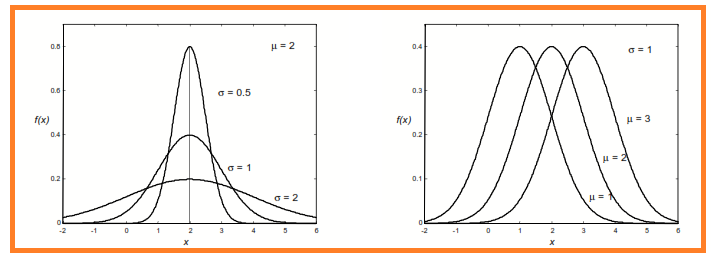
La distribuzione normale è completamente individuata dai parametri µ e σ , ossia in corrispondenza di ogni valore di µ e σ rimane specificata una diversa curva normale appartenente alla famiglia rappresentata dall’equazione (*).
Nella figure sotto si riportano i grafici della distribuzione normale per un dato valore di µ e per diversi valori di σ : a parità di valor medio le variazioni della forma caratteristica a campana della curva dipendono essenzialmente dal valore dello scarto quadratico medio, che dà informazioni su come i valori sono più o meno concentrati intorno alla media: infatti facendo variare σ si ottengono curve più o meno appiattite.
Nella seconda figura si riportano invece i grafici della distribuzione normale per un dato valore di σ e per diversi valori di µ: in questo caso le variazioni del valore di µ comportano solo una traslazione della curva.
Distribuzione normale standardizzata

Come già osservato, la distribuzione normale è una famiglia di distribuzioni in cui ogni membro è distinto dall’altro in base ai valori di µ e σ . La curva più importante della famiglia è la distribuzione normale standardizzata. Per ricavare questa distribuzione, data la variabile aleatoria X distribuita normalmente con media µ e varianza σ2, si passa alla nuova variabile aleatoria Z, detta variabile standardizzata, ponendo
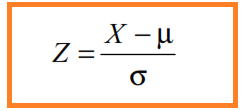
La trasformazione operata fa in modo che la media di Z sia 0 e la varianza 1.
La distribuzione di probabilità della variabile normale standardizzata Z è data da:

Nei grafici della figura 7, riproducenti la distribuzione normale standardizzata, indichiamo le aree comprese rispettivamente tra −1 e 1, tra −2 e 2 e tra −3 e 3, pari al 68.27%, al 95.44% e al 99.73% dell’area totale, che è 1. Questo significa che:
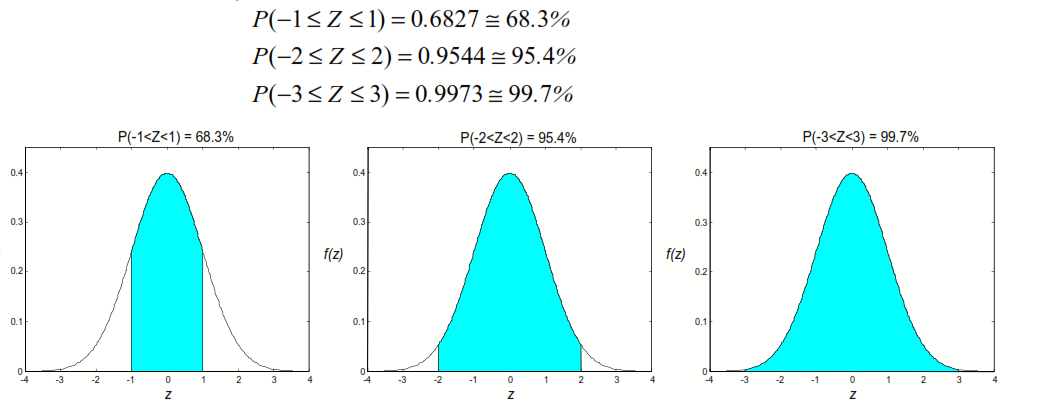
Tenendo conto che per la variabile normale standardizzata lo scarto quadratico medio è uguale a 1,dal primo grafico della figura precedente si deduce sostanzialmente che una variabile aleatoria distribuita normalmente ha probabilità del 68.3% di discostarsi dalla media per meno di σ ; analogamente dal secondo e dal terzo grafico si deduce che una variabile aleatoria normale ha probabilità del 95.4% di discostarsi dalla media per meno di 2σ e del 99.7% per meno di 3σ , cioè è quasi impossibile che si discosti dalla media per più di 3σ

Uso delle tavole della distribuzione normale
poiché la (*) individua una famiglia di distribuzioni, ed esistono infinite combinazioni dei parametri µ e σ che individuano una curva della famiglia, non è possibile predisporre un numero infinito, o almeno molto elevato, di tavole. Si ricorre perciò alla variabile aleatoria standardizzata: è sempre possibile trasformare una distribuzione normale di parametri µ e σ nella corrispondente distribuzione standardizzata per mezzo del cambiamento di
variabile:
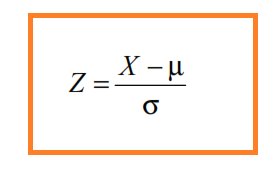
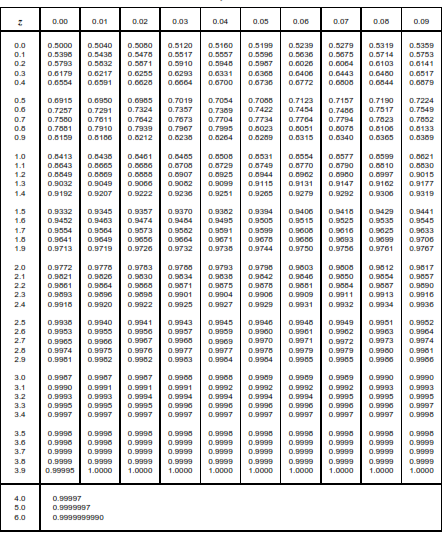
La tavola sotto fornisce il valore della funzione di distribuzione della variabile aleatoria standardizzata Z
F(z) = P ( Z<=z)
ossia il valore dell’area sottesa dalla curva normale standardizzata f (z) , a sinistra di un valore z assegnato;
Valgono alcune proprietà utili per l’uso delle tavole.
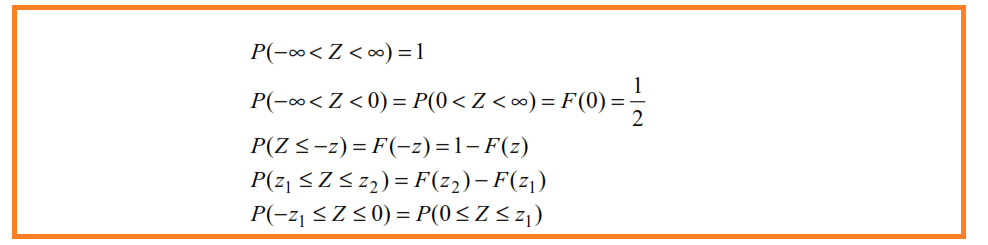
Esercizio 1:
Calcolare, usando la tavola della distribuzione normale standardizzata, la probabilità che una variabile aleatoria Z avente la distribuzione normale standardizzata assuma valori tali che
a − 087 <= Z <= 1.28
b − -0.34 <= Z <=0.62
c − Z>= 0.85
d − Z >= -0.65
Soluzione:
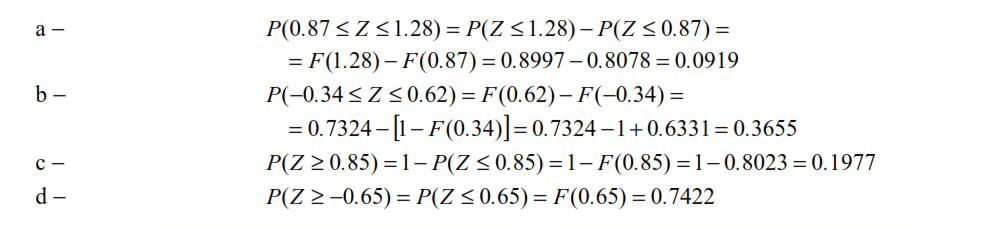
Esercizio 2:
Calcolare, usando la tavola della distribuzione normale standardizzata, la probabilità che una variabile aleatoria Z avente la distribuzione normale standardizzata assuma valori tali che:

Se la variabile aleatoria non è standardizzata, prima di poter usare le tavole si deve ricorrere al cambiamento di variabile , visto in precedenza, per standardizzarla.
Esercizio 3:
Sia X una variabile aleatoria avente distribuzione normale, con µ = 4.35 e σ = 0.59; trovare la probabilità
P(4 ≤ X ≤ 5) .

(324)
