Esercizi svolti sulle Formule di Taylor e Maclaurin

TAVOLA DEGLI SVILUPPI DI TAYLOR DELLE FUNZIONI ELEMENTARI PER x -> 0.

ESERCIZIO 1

Scrivere le formule di MacLaurin arrestate al sesto ordine delle funzioni:

SOLUZIONE

Ogni funzione in esame è composta di una funzione f(t) di cui si conosce la formula di MacLaurin e di un monomio g(x) (di secondo grado). Poiché in x₀ = 0 risulta t₀ = g(0) = 0, e f(g(x)) è una funzione che ammette derivate (continue) di ogni ordine, è possibile calcolare la formula di MacLaurin di f(g(x)) sostituendo t = g(x) nella formula di MacLaurin di f(t). In più, per avere una formula arrestata al sesto ordine di f(g(x)), basterà arrestare la formula di f(t) al terz’ordine.

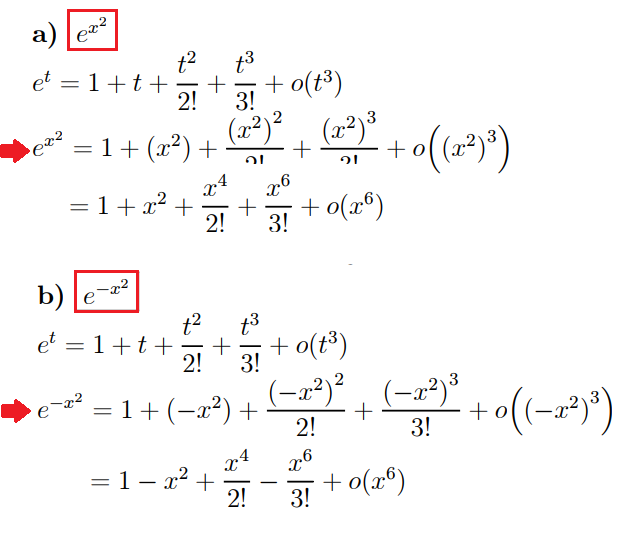
ESERCIZIO 2

Scrivere le formule di MacLaurin arrestate al terz’ordine della funzione:

(a) utilizzando la definizione
(b) vedendo e^x−x2 come prodotto di e^x e e^−x2 e utilizzando le formule precedentemente calcolate (a quale ordine bisogna arrestare il polinomio di MacLaurin di e^−x2 per essere sicuri di non trascurare infinitesimi significativi?)
(c) usando la formula di MacLaurin di e^t con t = x − x² (quali termini si possono trascurare?)

SOLUZIONE

Dobbiamo scrivere le formule di MacLaurin arrestate al terz’ordine della funzione, seguendo la definizione, la formula di MacLaurin si ottiene scrivendo le prime 3 derivate,  il loro valore per x₀ = 0 e desumendo il coefficiente di ogni x^k (che si ottiene dividendola derivata k-esima per k!): 

Quindi:

b)

Allora:

c)

Usando la formula di MacLaurin arrestata al terz’ordine di

ESERCIZIO 3

È vero che, per x che tende a 0, la funzione ln(1 − x + x²) + x − x² è o(x²)? Motivare l’affermazione.

SOLUZIONE

Per x che tende a 0, la funzione ln(1 − x + x²) + x − x² NON è o(x²).
Infatti sostituendo t = x−x² nella formula di MacLaurin di ln(1 + t) arrestata al second’ordine:

ESERCIZIO 4

Si può calcolare la formula di MacLaurin arrestata al second’ordine di e ^√x? Motivare l’affermazione.

SOLUZIONE

NON si può calcolare la formula di MacLaurin arrestata al second’ordine di e^√x.
Infatti la funzione in esame non è derivabile in x₀ = 0, non essendolo √x. Tuttavia continua a valere il limite notevole:

Qui trovi tutti i limiti notevoli

ESERCIZIO 5

Calcolare li seguente limite, prima utilizzando le formule di MacLaurin opportunamente arrestate e successivamente usando il teorema di de l’Hospital:

SOLUZIONE

Invece, usando il teorema di de l’Hospital,

ESERCIZIO 6

Calcolare li seguente limite, prima utilizzando le formule di MacLaurin opportunamente arrestate e successivamente usando il teorema di de l’Hospital:

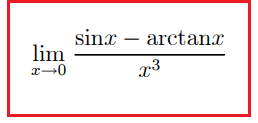
SOLUZIONE

Invece, usando il teorema di de l’Hospital,

ESERCIZIO 7

Calcolare li seguente limite, prima utilizzando le formule di MacLaurin opportunamente arrestate e successivamente usando il teorema di de l’Hospital:

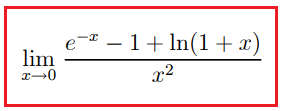
SOLUZIONE

Questo esercizio insegna che, in presenza di somme di funzioni ciascuna da approssimare con un polinomio, può non essere sufficiente arrestare le formule di Taylor all’ordine indicato ad esempio da un monomio presente al denominatore (o al numeratore), in quanto i primi addendi possono annullarsi vicendevolmente.

Invece, usando il teorema di de l’Hospital,

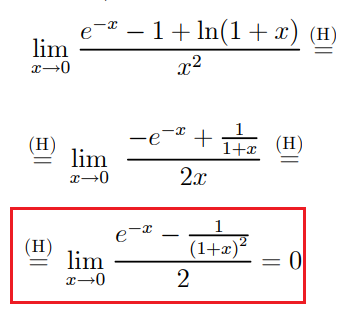
[elementor-template id=”10963″]

(34862)