RELAZIONI TRA DUE CARATTERI STATISTICI

RELAZIONI TRA DUE CARATTERI STATISTICI

Nell’ analisi di dati si è spesso interessati a studiare se tra due caratteri X e Y, che si presentano congiuntamente sulle unità statistiche che formano una data popolazione, si possa stabilire un qualche “legame” e, nel caso, quale sia il grado di tale relazione. Si possono avere casi in cui la conoscenza di una delle due variabili non dà alcuna informazione sull’ altra (indipendenza) e casi di perfetta dipendenza in cui una delle variabili determina anche l’altra. Si tratta ovviamente di casi limite, nella pratica ci si può più o meno “avvicinare” alla situazione di indipendenza. Il grado di relazione fra due variabili viene misurato con vari indici statistici che, in sostanza, sono opportune distanze tra la situazione effettivamente osservata e quella relativa al caso di indipendenza. Si ottengono così misure di associazione. Se le variabili sono entrambe quantitative è possibile studiare i legami di interdipendenza tramite la correlazione e la dipendenza di una delle variabili dall’ altra con l’analisi di regressione.

Associazione tra variabili statistiche

ESEMPIO:

Un collettivo di 219 studenti, 119 maschi (M) e 100 femmine (F), viene sottoposto ad un test attitudinale. Le attitudini prese in esame sono: A: discipline artistiche; B: discipline umanistiche; C: materie scientifiche.

Ci si pone il problema di studiare l’associazione tra sesso e attitudine.

In prima fase si può osservare ch e le percentuali di maschi e di femmine nel collettivo preso in esame sono:

% di M = 119 / 219 = 54 % e % di F = 100 / 219 = 46 %.

Se ci fosse indipendenza tra sesso e attitudine si dovrebbe riscontrare le stesse % di M e F per le attitudini A, B e C. Sotto l’ipotesi di indipendenza, allora, si dovrebbe ottenere un valore atteso o teorico di frequenza e_MA per i maschi con l’attitudine A tale che:

In modo analogo possono essere determinate le altre 5 frequenze teoriche:

Sulla base di tali risultati è possibile costruire la Tab 2 seguente.

L’associazione tra le due variabili può essere analizzata considerando una “distanza” tra le frequenze osservate (Tab. 1) e quelle teoriche (Tab. 2). All’uopo si considerano le differenze tra tali frequenze, come riportato in Tab. 3:

e si introduce l’indice chi-quadrato χ2 come misura di associazione:

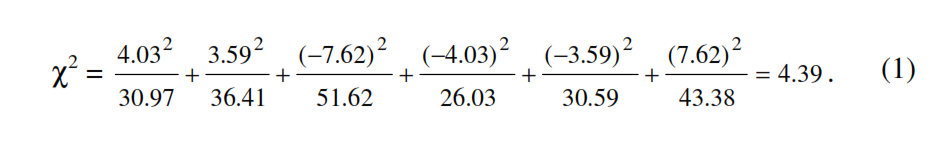
Come si può osservare l’indice è costituito dalla somma di 6 frazioni che presentano a numeratore i quadrati delle differenze tra le frequenze osservate e quelle teoriche e a denominatore le frequenze teoriche.

Utilizzando il linguaggio R, i dati possono essere memorizzati in una matrice:

La costruzione dell’indice χ2 è generalizzabile al caso di due caratteri X e Y, con modalità x1, x2, x3, …, xr e y1, y2, y3, …yc, rilevati contemporaneamente su n unità statistiche. In tal caso la tabella delle frequenze osservate o_ij (per i = 1,2,…,r e j = 1,2,…,c ) assume la forma della tabella di contingenza Tab. 4 formata da r righe e c colonne:

La tabella di contingenza

Nella tabella le quantità:

sono le frequenze marginali della X e, rispettivamente, della Y.

Sotto l’ipotesi di indipendenza di X e Y, la frequenza teorica relativa alla modalità x_i di X e alla modalità y_j va determinate secondo la:

Successivamente vanno calcolate le differenze tra le frequenze osservate e quelle teoriche o_ij-e_ij e, quindi, analogamente alla (1), l’indice chi-quadrato:

L’indice chi-quadrato

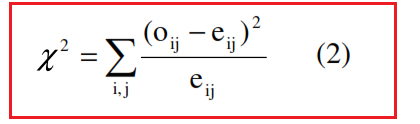
Si osservi ora che l’indice χ2 dipende dalla numerosità n del collettivo, il suo valore, a parità di associazione tra i due caratteri presi in esame, aumenta all’aumentare di n. Si può allora prendere in esame l’indice di contingenza quadratica media:

L’indice di contingenza quadratica media:

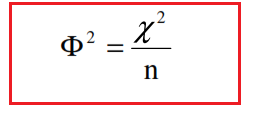
e assumere come misura di associazione la radice quadrata Φ di tale quantità. Così per l’esempio 1 si ottiene:

Intervallo di variazione dell’indice di contingenza quadratica media

un valore prossimo a 0 porta ad escludere un’associazione tra i due caratteri. Un valore di Φ pari a 0.14 porterebbe ad ipotizzare una non dipendenza tra il Sesso e l’Attitudine, tuttavia la problematica va esaminata con più attenzione facendo riferimento anche ad ulteriori strumenti di analisi.

L’indice di associazione normalizzato V di Cramer:

Spesso, nella misura di associazione, si fa riferimento anche all’indice di associazione normalizzato V di Cramer:

La V varia tra 0 e 1 ;

valori prossimi a 1 denotano una forte associazione tra le due variabili, ma tuttavia non danno indicazioni sulle “modalità” di associazione. Per l’esempio 1 si ottiene: V = 0.14, valore coincidente, in questo caso, con quello di Φ in quanto il minimo viene calcolato tra (2−1) e (3−1).

Utilizzando R:

PER CONCLUDERE:

ESEMPIO:

Calcolo della misura di associazione:

 

ESEMPIO:

Statistica

Distribuzione binomiale: esercizio risolto con Excel

(1754)