
Approccio del p-value alla verifica di ipotesi
Esiste un altro approccio alla verifica di ipotesi: l’approccio del p-value.
Il p-value rappresenta la probabilità di osservare un valore della statistica test uguale o più estremo del valore che si calcola a partire dal campione, quando l’ipotesi H0 è vera.
Un p-value basso porta a rifiutare l’ipotesi nulla H0.
Il p-value è anche chiamato livello di significatività osservato, in quanto coincide con il più piccolo livello di significatività in corrispondenza del quale H0 è rifiutata.
In base all’approccio del p-value, la regola decisionale per rifiutare H0 è la seguente:
- Se il p-value è ≥ α, l’ipotesi nulla non è rifiutata.
- Se il p-value è < α, l’ipotesi nulla è rifiutata.
Torniamo ancora una volta all’esempio relativo alla produzione delle scatole di cereali. Nel verificare se il peso medio dei cereali contenuti nelle scatole è uguale a 368 grammi, abbiamo ottenuto un valore di Z uguale a 1.50 e non abbiamo rifiutato l’ipotesi, perché 1.50 è maggiore del valore critico più piccolo –1.96 e minore di quello più grande +1.96.
Risolviamo, ora, questo problema di verifica di ipotesi facendo ricorso all’approccio del p-value. Per questo test a due code, dobbiamo, in base alla definizione del p-value, calcolare la probabilità di osservare un valore della statistica test uguale o più estremo di 1.50.
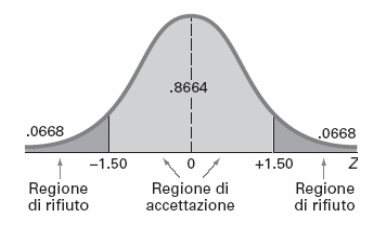
Si tratta, più precisamente, di calcolare la probabilità che Z assuma un valore maggiore di 1.50 oppure minore di –1.50.
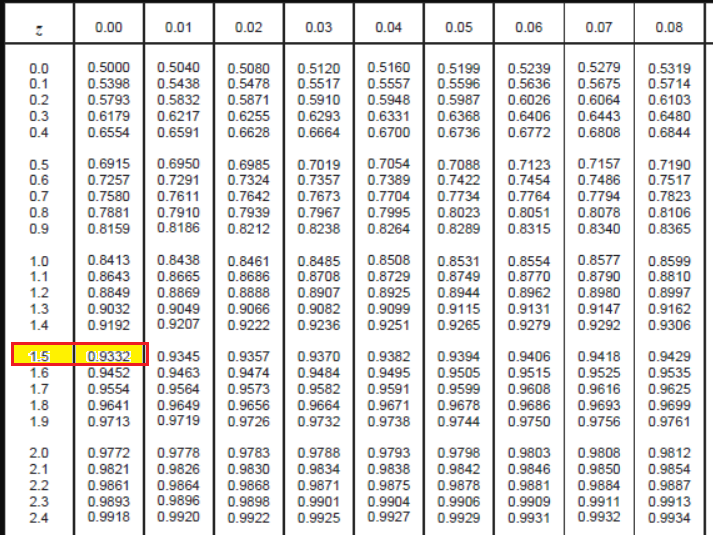
In base alla Tavola, la probabilità che Z assuma un valore minore di –1.50 è 0.0668, mentre la probabilità che Z assuma un valore minore di +1.50 è 0.9332, quindi la probabilità che Z assuma un valore maggiore di +1.50 è 1 – 0.9332 = 0.0668.
Pertanto il p-value per questo test a due code è 0.0668 + 0.0668 = 0.1336
Legame tra intervalli di confidenza e verifica di ipotesi
In questo e nell’articolo precedente abbiamo preso in considerazione i due elementi principali dell’inferenza statistica – gli intervalli di confidenza e la verifica di ipotesi.
Sebbene abbiano una stessa base concettuale, essi sono utilizzati per scopi diversi: gli intervalli di confidenza sono stati usati per stimare i parametri della popolazione, mentre la verifica di ipotesi viene impiegata per poter prendere delle decisioni che dipendono dai valori dei parametri.
Tuttavia è importante sottolineare che anche gli intervalli di confidenza possono consentire di valutare se un parametro è minore, maggiore o diverso da un certo valore: anziché sottoporre a verifica l’ipotesi µ=368 possiamo risolvere il problema costruendo un intervallo di confidenza per la media µ. In questo caso accettiamo l’ipotesi nulla se il valore ipotizzato è compreso nell’intervallo costruito, perché tale valore non può essere considerato insolito alla luce dei dati osservati. D’altronde, l’ipotesi nulla va rifiutata se il valore ipotizzato non cade nell’intervallo costruito, perché tale valore risulta insolito alla luce dei dati.
Con riferimento al problema considerato ( quello delle scatote di cereali,ricordate?), sulla base dell’equazione (1),

l’intervallo di confidenza è costruito ponendo:
n= 25, = 372.5 grammi,
σ = 15 grammi.
Per un livello di significatività del 95% (corrispondente al livello di significatività del test α=0.05), avremo:

Poiché l’intervallo comprende il valore ipotizzato di 368 grammi, non rifiutiamo l’ipotesi nulla e concludiamo che non c’è motivo per ritenere che il peso medio dei cereali contenuti nelle scatole sia diverso da 368 grammi.
I test ad una coda
Nel paragrafo precedente abbiamo considerato i cosiddetti test a due code ad esempio abbiamo contrapposto all’ipotesi nulla μ = 368 grammi l’ipotesi alternativa μ ≠ 368. Tale ipotesi si riferisce a due eventualità: o il peso medio è minore di 368 oppure è maggiore di 368. Per questo motivo, la regione critica si divide nelle due code della distribuzione della media campionaria.
In alcune situazioni, tuttavia, l’ipotesi alternativa suppone che il parametro sia maggiore o minore di un valore specificato (ci si focalizza in una direzione particolare). Per esempio, il direttore dell’area finanziaria può essere interessato all’eventualità che il peso dei cereali contenuti ecceda i 368 grammi, perché in tal caso, essendo il prezzo delle scatole basato su un peso di 368 grammi, la società subirebbe delle perdite. In questo caso si intende stabilire se il peso medio è superiore a 368 grammi.
L’ipotesi nulla e l’ipotesi alternativa in questo caso sono specificate rispettivamente:
H0: µ ≤ 368
H1: µ >368
La regione di rifiuto in questo caso è interamente racchiusa nella coda destra della distribuzione della media campionaria, perché rifiutiamo l’ipotesi nulla H0 solo se la media è significativamente superiore a 368 grammi. Quando la regione di rifiuto è contenuta per intero in una coda della distribuzione della statistica test, si parla di test a una coda.
Fissato il livello di significatività α, possiamo individuare, anche in questo caso, il valore critico di Zα.
Nel caso
H0: µ ≥ 368
contro
H1: µ < 368
possiamo individuare il valore critico di Zα come segue:
Poiché la regione critica è contenuta nella coda di sinistra della distribuzione normale standardizzata e corrisponde a un’area di 0.05, il valore critico lascia alla sua sinistra una massa pari a 0.05; pertanto tale valore è −1.645 (media di −1.64 e −1.65).

Il test di ipotesi t per la media ( σ non noto)
In molte applicazioni lo scarto quadratico medio della popolazione σ non è noto ed è quindi necessario stimarlo con lo scarto quadratico medio del campione S.
Se si assume che la popolazione abbia distribuzione normale allora la media campionaria si distribuisce secondo una t di Student con (n−1) gradi di libertà

Se variabile casuale X non ha una distribuzione normale la statistica t ha comunque approssimativamente una distribuzione t di Student in virtù del Teorema del Limite Centrale.
Facciamo un esempio:
Si consideri un campione di fatture per valutare se l’ammontare medio delle fatture è stato uguale a $120.
- H0: µ = 120 H1: µ ≠ 120
- α=0.05 e n= 12
- poiché σ non è noto la statistica test è t con n−1 gradi di libertà
- il test è a due code e i valori critici si determinano dalla Tavola:


dati i valori delle 12 fatture campionate
108.98 152.22 111.45 110.59 127.46 107.26 93.32 91.97 111.56 75.71 128.58 135.11
si ottiene
X = 112.85 e S = 20.80
e quindi

poiché
−2.201 < t = −1.19 < +2.201 l’ipotesi nulla non va rifiutata
[elementor-template id=”10808″]
[elementor-template id=”10688″]
(538)
