
Indice
Il rango di una matrice
Premettiamo la seguente definizione.
Minore di una matrice
Se A è una matrice di ordine m x n e se r è un numero naturale minore o uguale sia di m che di n, dicesi minore estratto di ordine r della matrice A, ogni determinante formato da r righe e da r colonne di A.
I minori estratti di una matrice A sono, in generale, più di uno.
As esempio, se

Ciò posto, possiamo dare la seguente definizione:
Rango di una matrice
Se A è una matrice di ordine m x n, dicesi rango o caratteristica di A il massimo ordine fra tutti i minori estratti diversi da zero.
Il rango di una matrice A si indica con rang(A) o car(A).
Pertanto, dire che rang(A) = r, vuol dire che:
1) esiste almeno un determinante estratto di ordine r diverso da zero;
2) ogni determinante estratto di ordine maggiore di r è uguale a zero.
Sussiste il seguente metodo, detto metodo degli orlati o di Kroneker, per calcolare il rango di una matrice.
Esso consiste dei seguenti passi:
1) si sceglie un minore estratto di ordine 1, diverso da zero;
2) si orla tale minore estratto in tutti i modi possibili con un’altra riga e un’altra colonna: se tutti i determinanti del 2° ordine così ottenuti sono nulli, allora il rango della matrice è 1;
3) se, invece, esiste un determinante del 2° ordine diverso da zero, lo si orla con un’altra riga e un’altra colonna, ottenendo un minore estratto del terzo ordine: se tutti i determinanti così ottenuti sono nulli, allora il rango è 2, altrimenti si procede come al passo precedente.
ESEMPIO:
Calcolare il rango della matrice:

Osserviamo preliminarmente che poiché A è una matrice 3×4, il suo rango può essere al massimo uguale a 3.
Consideriamo il minore estratto:

Orliamo tale elemento con la seconda riga e la seconda colonna ottenendo:

e, quindi, il rang(A) ≥ 2.
Orliamo tale estratto del 2° ordine con la terza riga e la terza colonna:

Poiché non esistono minori di ordine > 3, si conclude che rang(A) = 3.
PROPRIETA’ DEL RANGO DELLA MATRICE
Preposizione 1 :
Se A e B sono due matrici di tipo rispettivamente (m,p) ed (p,n) e se C è la matrice prodotto A ∙ B, allora risulta
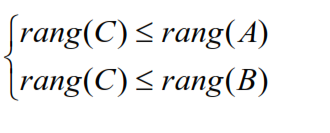
Preposizione 2 :
Il rango di una matrice non cambia se essa viene moltiplicata a sinistra o a destra per una matrice non singolare.
(500)
