
Dicesi sistema lineare di m equazioni in n incognite ogni sistema del tipo:

La matrice:
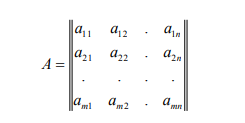
dicesi matrice dei coefficienti o matrice incompleta del sistema, mentre la matrice

ottenuta aggiungendo alla matrice dei soli coefficienti la colonna formata dai termini noti si dice matrice completa del sistema.
In generale, il numero m di equazioni di un sistema è diverso dal numero n delle incognite.
Osserviamo che se indichiamo con A la matrice dei coefficienti, con X il vettore colonna delle incognite e con B il vettore colonna dei termini noti, ogni sistema lineare si può indicare anche nella forma compatta
A x X = B.
In tal modo è possibile considerare il sistema come una equazione, equazione matriciale, e applicare ad essa le operazioni fra matrici, purché si tenga conto che non vale né la proprietà commutativa né la legge di annullamento del prodotto.
La forma
A x X = B
dicesi forma matriciale del sistema.
DEFINIZIONE
Dicesi soluzione del sistema ogni n-pla di numeri (x1, x2, …, xn) che soddisfa tutte le equazioni del sistema.
DEFINIZIONE ( SISTEMA DI KRAMER):
Un sistema lineare si dice sistema di Kramer se:
1) il numero delle equazioni è uguale al numero delle incognite, ovvero se m = n;
2) la matrice incompleta del sistema è non singolare, ovvero se det(A)≠0.
Per i sistemi di Kramer sussiste il seguente fondamentale teorema:
Teorema di Kramer
Se A x X = B è un sistema di Kramer, cioè avente m = n e det(A) ≠ 0, allora esso è determinato e l’unica soluzione è data da:

dove D è il determinante della matrice incompleta dei soli coefficienti (D = det(A)) e Di è il determinante ottenuto da D sostituendo la i-ma colonna con la colonna dei termini noti.
Spiegazione:

Le frazioni che esprimono la soluzione (x; y) hanno senso, perché stiamo supponendo D = ab1 -a1b ≠0.
Se D≠ 0, la soluzione esiste: il sistema è determinato.
Se D = 0, i casi sono due:
● se Dx = 0 e Dy =0, il sistema è indeterminato;
● se Dx≠ 0 oppure Dy ≠ 0, il sistema è impossibile.
ESEMPIO:

ESEMPIO:

ESEMPIO:

(1073)
