I problemi di costi e ricavo

Nei problemi di ottimizzazione bisogna trovare la soluzione ottimale in base a un dato criterio (massimizzare un profitto o minimizzare un costo, per esempio), determinando il massimo o il minimo di una opportuna funzione.
Il costo di ogni bene prodotto o acquistato dipende dalla combinazione di molti fattori: il costo delle materie prime, della manodopera, dei macchinari, eccetera. I costi si dividono in due categorie.

Costi  Fissi e Costi Variabili

I costi fissi (C_F) non variano al variare della quantità prodotta o acquistata; i costi variabili (C_V), invece, variano al variare della quantità prodotta o acquistata.

Esempi di costi fissi sono le spese per l’affitto dei locali, lo stipendio dei dipendenti e le spese di assicurazione.

Esempi di costi variabili sono le spese per l’acquisto delle materie prime, per la manutenzione degli impianti e per il consumo energetico.

Costi Totali

l costo totale (C_T ) è la somma dei costi fissi e dei costi variabili:

C_T = C_F + C_V

Ricavi

Il ricavo (R) è il denaro che si trae dalla vendita di un prodotto. È dato dalla formula

R = p · x

dove p è il prezzo di vendita di un singolo oggetto e x il numero di oggetti venduti.

Il Profitto

Il profitto (o guadagno) è l’utile realizzato dall’azienda. È dato dalla formula

P = R − C_T

e quindi si calcola sottraendo il costo totale dal ricavo.

Si può rappresentare graficamente l’andamento del profitto in funzione della quantità di beni venduti (grafico del profitto), oppure si possono rappresentare in uno stesso piano cartesiano l’andamento dei costi e del ricavo (diagramma di redditività). In questi grafici si possono individuare alcuni elementi essenziali:
• la zona di perdita, in cui il ricavo è minore del costo totale
• la zona di utile, in cui il ricavo è maggiore del costo totale
• il punto di pareggio (Break Even Point, in inglese, spesso denotato con BEP), che divide la zona di perdita dalla zona di utile, e che corrisponde al valore della quantità di beni venduti per cui ricavo e costo totale si equivalgono.

ESERCIZIO 1

Un commerciante acquista olio d’oliva al costo di 7 euro al litro e lo rivende a 12 euro al litro. Per il trasporto sostiene costi fissi giornalieri di 60 euro. Descrivi l’andamento del profitto giornaliero in funzione dei litri d’olio venduti.

SOLUZIONE

Indichiamo con x i litri d’olio venduti in un giorno. Non ci sono vincoli tecnici: il commerciante può vendere tutto l’olio che i suoi clienti gli chiedono. L’unico vincolo cui è soggetto x è il “vincolo di segno”:

x ⩾ 0

I costi fissi (indipendenti dal numero di litri venduti) sono di 60 euro al giorno: C_F = 60
I costi variabili sono di 7 euro al litro per il numero x di litri venduti: C_V = 7x
Il costo totale è la somma dei costi fissi e dei costi variabili: C_T = 7x + 60

Il ricavo è di 12 euro al litro per il numero x di litri venduti: R = 12x
Il profitto è dato dal ricavo meno il costo totale P = R − C_T = 12x − (7x + 60) = 5x − 60

Poiché tutte le funzioni in gioco sono lineari, i loro grafici sono delle rette. Per tracciare il grafico della funzione profitto determiniamo le coordinate del punto d’intersezione del grafico con l’asse x, risolvendo il sistema:

Quindi il punto di intersezione è (12, 0).

Grafico del profitto

 

• se vende meno di 12 litri d’olio, cioè se 0 ⩽ x < 12, il commerciante è inperdita in quanto per tali valori la funzione profitto è negativa
• x  = 12 è il punto di pareggio
• per tutti i valori superiori a 12 il commerciante ha un profitto positivo: quanto più grande è x > 12, tanto più grande è il profitto

Diagramma di redditività

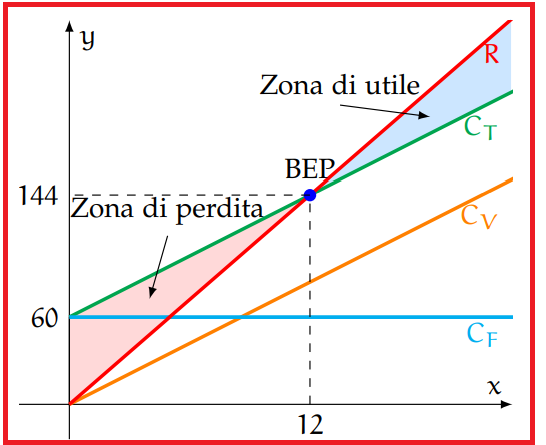
In alternativa, il problema si può risolvere costruendo il diagramma di redditività. La figura rappresenta le rette grafico delle funzioni CF, C_V, C_T ed R. Per determinare il punto di pareggio troviamo il punto di intersezione tra la funzione che rappresenta il costo totale e la funzione che rappresenta il ricavo, risolvendo il sistema:

Il punto di pareggio si ha dunque per x = 12. Quindi:
• se 0 ⩽ x < 12 il commerciante è in perdita
• se x = 12 il commerciante non ha né profitto né perdita
• se x > 12 il commerciante ha un profitto positivo
Le conclusioni coincidono con quelle trovate in precedenza.

Un problema di ottimizzazione con un vincolo tecnico

ESERCIZIO 2

Consideriamo il problema precedente, aggiungendo la condizione che il commerciante può trasportare al massimo 20 litri d’olio al giorno. Quanti litri d’olio deve vendere per avere il massimo profitto? Qual è il massimo profitto? A quanti litri venduti si ha il punto di pareggio?

SOLUZIONE

L’unica differenza rispetto all’esercizio precedente è la presenza del vincolo tecnico x ≤ 20. Determiniamo il punto di intersezione del grafico della funzione profitto con la retta x = 20:

Quindi il punto di intersezione è (20, 40).

La figura rappresenta il grafico della funzione profitto. Abbiamo che:
• se vende meno di 12 litri d’olio, cioè se 0 ⩽ x < 12, il commerciante è in perdita
• per x = 12 il commerciante non ha né utile né perdita (break even point)
• per tutti i valori superiori a 12 fino al massimo trasportabile 20, cioè per 12 <x ⩽ 20, il commerciante ha un profitto positivo
• il profitto è crescente e raggiunge il massimo, pari a 40 euro, in corrispondenza della quantità d’olio massima trasportabile, cioè per x =20

In alternativa, il problema si può risolvere costruendo il diagramma di redditività.

 

La figura rappresenta le rette grafico delle funzioni C_F, C_V, C_T ed R. Il massimo profitto si ha quando la differenza tra ricavo e costo è massima, ovvero per x = 20, per cui
R(20) − P(20) = 12 · 20 − (7 · 20 + 60) = 240 − 200 = 40
e l’analisi economica coincide con quella fatta in precedenza.

(7055)