I problemi di scelta

Si dicono problemi di scelta i problemi in cui viene chiesto di operare, fra varie alternative, la scelta più conveniente (secondo un determinato criterio, per esempio quello di massimizzare un profitto o minimizzare una spesa).

Nei problemi ad una sola alternativa, lo scopo è quello di determinare un valore della variabile x che renda minima o massima la funzione obiettivo.

Vi sono anche dei problemi in cui lo scopo è quello di scegliere l’alternativa più conveniente al variare di x  tra funzioni che esprimono , per Iesempio procedimenti differenti per la fabbricazione di un prodotto, oppure tariffe diverse per il trasporto di merce.
Per arrivare alla soluzione di questi problemi sarà necessario:

• scrivere il modello matematico individuato dalle funzioni obiettivo e dai vincoli;
• determinare i punti di intersezione tra le funzioni obiettivo, che rappresentano i punti di indifferenza;
• rappresentare graficamente, su un unico piano cartesiano, le diverse alternative;
• determinare dal grafico gli intervalli per i quali conviene una o l’altra alternativa.

Problema di minimo

ESEMPIO 1
Per il trasporto di una merce un’impresa può ricorrere a due differenti ditte per il trasporto.
La prima (A) chiede un fisso di 50 euro per ogni spedizione più un costo di 0,5 euro per ogni chilometro del tragitto;
La seconda (B) chiede un fisso di 30 euro più un costo per chilometro pari a 1 euro.
Con quali modalità effettuare la scelta tra le due offerte?

E’ un problema di costi.

Quindi si scrive il modello matematico: le due funzioni del costo totale e i vincoli.

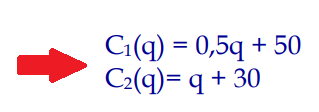
In questo caso c’è solo vincolo di segno: q ≥ 0

Per determinare il punto di indifferenza, bisogna mettere a sistema le due funzioni:

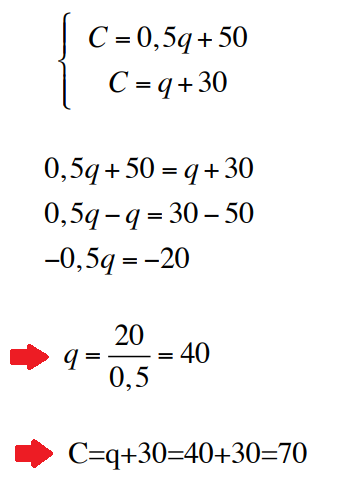
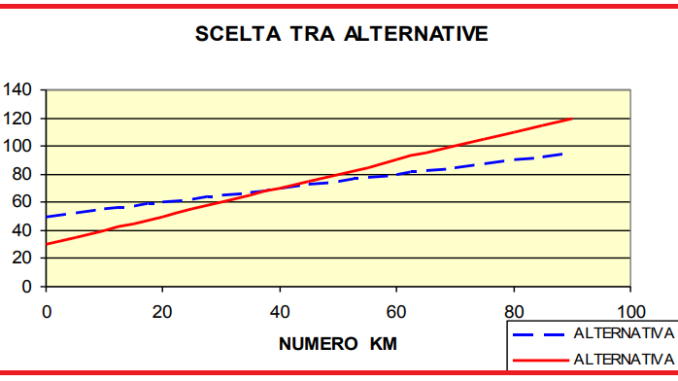
Poi si rappresentano graficamente le due funzioni di costo totale con il punto di indifferenza trovato:

Si osserva che
• per q < 40 km conviene l’offerta B, in quanto più bassa
• per q > 40 km conviene l’offerta A, in quanto più bassa
• per q = 40 km si ha un punto di indifferenza, ossia le due offerte si equivalgono

ESEMPIO 2

Per trasportare della merce, ci si può servire di 3 imprese A, B, C, le quali offrono i loro servizi alle seguenti condizioni :
A) 10 euro a tonnellata
B) 120 euro fissi, più 6 euro a tonnellata
C) 200 euro fissi, più 5 a tonnellata
Determinare quando sarà più conveniente servirsi di ciascuna delle tre imprese.

In questo caso si hanno tre possibili alternative tra cui scegliere, per cui bisognerà trovare tre p eventuali punti di indifferenza, una volta mettendo a sistema A e B, una volta B e C e una volta A e C.

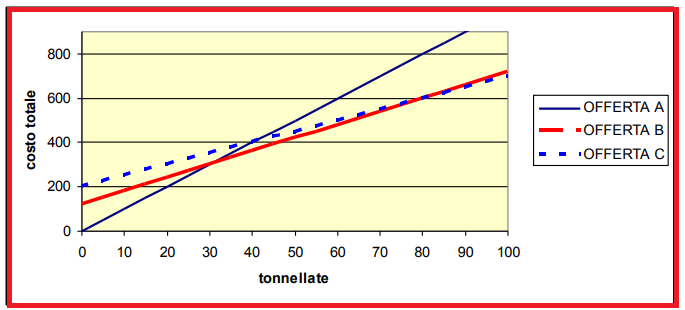
⇒  Fino a 30 t conviene A
     Da 30 t a 80 t conviene B
Oltre le 80 t conviene C

ESERCIZIO 1

A un promotore di polizze assicurative vengono proposti due tipi di stipendio:
• contratto A: 1000 euro al mese più 50 euro per ogni polizza stipulata
• contratto B: 500 euro al mese più 100 euro per ogni polizza stipulata
Determina il contratto più conveniente.

SOLUZIONE

È chiaro che non potrà esserci una scelta più conveniente “in assoluto”: la maggiore o minore convenienza di un contratto dipendono infatti dal numero di polizze stipulate dall’assicuratore. Ci proponiamo perciò di determinare qual è la scelta più conveniente a seconda del numero di polizze stipulate.

Costruiamo il modello matematico del problema.

Indichiamo con x il numero (intero ⩾ 0) di polizze stipulate in un mese e con y il corrispondente stipendio in euro:
• lo stipendio relativo al contratto A è espresso dalla funzione y = 50x + 1000
• lo stipendio relativo al contratto B è espresso dalla funzione y = 100x + 500

Tracciando i grafici delle due funzioni e confrontandoli, potremo stabilire qual è la scelta più conveniente.

Poiché le due funzioni sono lineari, i loro grafici sono delle rette. Per comodità tracciamo queste due rette come se x fosse una variabile reale (anche se i punti delle rette che rappresentano il problema sono in realtà solo quelli a coordinate intere, dato che il dominio di x è costituito dall’insieme degli interi ⩾ 0).

problema di “massimo stipendio”

 

Le figure sopra riportano le rette grafico delle due funzioni, in un opportuno sistema di riferimento cartesiano.
Per risolvere il problema determiniamo le coordinate del punto d’intersezione P delle rette che abbiamo tracciato in figura.

A tal fine risolviamo il seguente sistema:

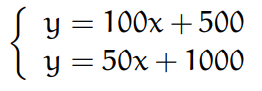
da cui:

Quindi il punto di intersezione è P(10, 1500).
La linea di “massimo stipendio” è evidenziata in figura con un tratto ondulato: essa è costituita per x < 10 dalla retta corrispondente al contratto A e per x > 10 dalla retta corrispondente al contratto B.

In conclusione:
• per un numero di polizze inferiore a 10 conviene il contratto A
• per un numero di polizze superiore a 10 conviene il contratto B
• per esattamente 10 polizze è indifferente il contratto A o B

ESERCIZIO 2

Paolo vuole frequentare una palestra per un mese e deve scegliere tra le seguenti tre proposte:
• palestra A: costo fisso d’iscrizione di 15 euro, più 7 euro per ogni ingresso
• palestra B: costo fisso d’iscrizione di 25 euro, più 5 euro per ogni ingresso
• palestra C: abbonamento mensile di 85 euro, senza limiti di ingresso
Qual è la scelta più conveniente per Paolo?

SOLUZIONE

Indichiamo con x il numero di ingressi alla palestra che Paolo intende effettuare in un mese e con y la corrispondente spesa in euro: x potrà variar nell’insieme dei numeri interi compresi tra 0 e 30.

Abbiamo che:
• la spesa per frequentare la palestra A è espressa dalla funzione y = 7x + 15
• la spesa per frequentare la palestra B è espressa dalla funzione y = 5x + 25
• la spesa per frequentare la palestra C è espressa dalla funzione y = 85

Tracciando i grafici delle tre funzioni e confrontandoli, potremo stabilire qual è la scelta più conveniente.
Poiché le tre funzioni sono lineari, i loro grafici sono delle rette.

Come al solito, per comodità tracciamo queste tre rette come se x fosse una variabile reale (anche se i punti delle rette che rappresentano il problema sono in realtà solo quelli a coordinate intere, perché il dominio di x è costituito dai numeri interi compresi tra 0 e 30).

problema di “minimo costo”

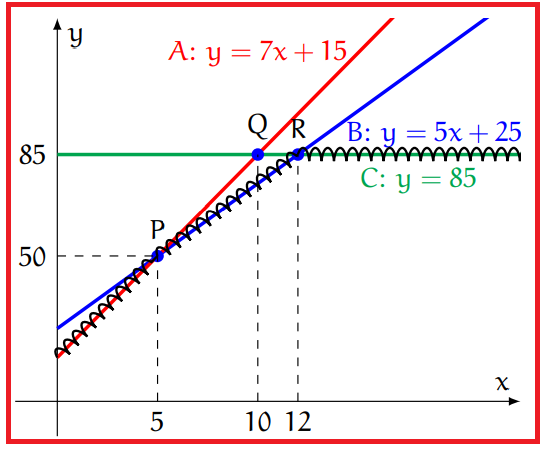
La figura riporta le rette grafico delle tre funzioni, in un opportuno sistema di riferimento cartesiano.
Determiniamo le coordinate di P (punto di intersezione tra le rette A e B), Q (intersezione tra A e C) e R (intersezione tra B e C), risolvendo i sistemi

Quindi i punti di intersezione sono P(5, 50), Q(10, 85) e R(12, 85).
La linea di “minimo costo” è quella evidenziata nella figura  con un tratto ondulato:

essa è costituita per x < 5 dalla retta corrispondente alla palestra A, per 5 < x < 12 dalla retta corrispondente alla palestra B e per x > 12 dalla retta corrispondente alla palestra C.

In conclusione:

• per un numero di ingressi inferiore a 5 conviene scegliere la palestra A
• per un numero di ingressi compreso tra 5 e 12 conviene scegliere la palestra B
• per un numero di ingressi superiore a 12 conviene scegliere la palestra C
• per esattamente 5 ingressi è indifferente scegliere la palestra A o la B
• per esattamente 12 ingressi è indifferente scegliere la palestra B o la C

(12382)