Cos’ è un problema di massimo e minimo

Capita spesso di trovarsi di fronte a questioni che riguardano scelte di ottimizzazione:
1. Quale è il percorso più breve fra due città?
2. Quale forma dovrebbe avere una barca per offrire la minima resistenza all’acqua?
3. Quando un’azienda realizza il massimo guadagno rendendo minimo l’impiego delle risorse a sua disposizione?
4. Quale forma deve avere uno scaldabagno per disperdere la minima quantità di calore?
Allora la domanda “che cosa è un problema di massimo e minimo”, trova la sua risposta in modo naturale: c’è sempre una grandezza di varia natura che cambia e occorre trovare in quali circostanze essa è massima o minima a seconda della situazione problematica che si intende risolvere.

ESEMPIO

IL PERCORSO PIÙ BREVE TRA DUE VILLAGGI. ILTEOREMA DI ERONE

Partiamo da un problema:

dalla stessa parte di un fiume si trova una pianura in cui sono situati due villaggi. Una persona deve andare da un villaggio all’altro attingendo lungo il cammino acqua dal fiume.
Quale è il cammino più breve che dovrà fare?

Cerchiamo di formulare il problema in termini matematici.
Innanzi tutto supponiamo che tratto di fiume interessato sia rettilineo e assimiliamo i due villaggi a due punti.
Allora arriviamo alla formulazione matematica del problema che prende il nome di Teorema di Erone:
dati una retta l e due punti P e Q dalla stessa parte di l, per quale punto R di l è minima la distanza PR+QR ?
Il problema si risolve bene attraverso una dimostrazione geometrica.

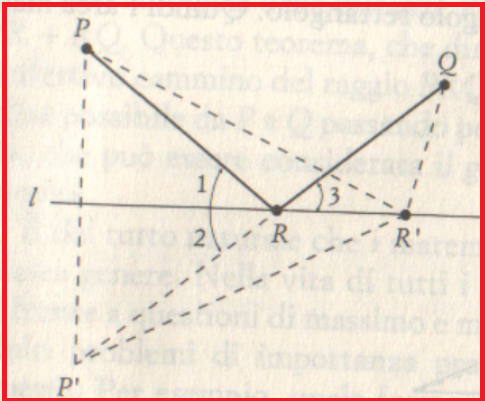
Consideriamo il punto P’ simmetrico di P rispetto alla retta l.
Congiungiamo P’ con Q e chiamiamo R il punto di intersezione fra l e il segmento P’Q.
Dimostriamo che R è il punto cercato.
Infatti preso un qualsiasi altro punto R’ della retta l dobbiamo dimostrare che si ha:

PR+QR<PR’+QR’.

Ricordando la proprietà dell’asse di un segmento e le disuguaglianze nei triangoli otteniamo:

PR+QR=P’R+QR=P’Q<P’R’+R’Q=PR’+QR’.

Il punto R così come è costruito è il punto cercato.
Andiamo a vedere meglio quali sono le proprietà di R.
Gli angoli 1 e 2 sono congruenti perché R è sull’asse di PP’,
Gli angoli 2 e 3 sono congruenti perché opposti al vertice, quindi risultano congruenti anche 1 e 3.
Allora R è tale che gli angoli che i segmenti PR e QR formano con la retta l sono congruenti.

I problemi di massimo e minimo nella storia della Matematica

Sappiamo trovare una situazione analoga che ci richiama il problema appena visto?
La situazione la si riscontra, per esempio, in fisica nella riflessione di un raggio luminoso emesso da una sorgente puntiforme su uno specchio piano (con la sorgente dalla stessa parte della superficie riflettente).

ESEMPIO

IL TRIANGOLO DI AREA MASSIMA

Il problema è il seguente:

fra i triangoli aventi due lati di misura assegnata, quale è quello di area massima?

Procediamo innanzi tutto per via intuitiva.
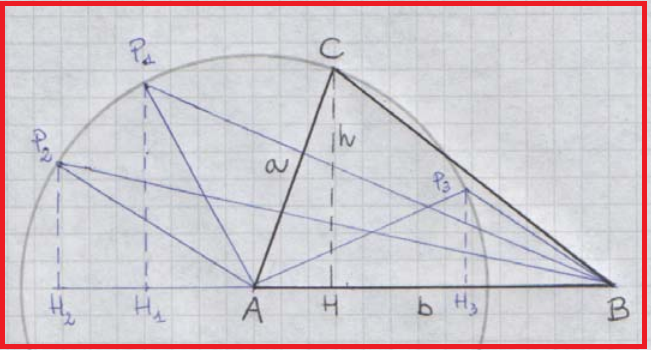
Consideriamo un triangolo qualsiasi e indichiamo per comodità a e b sia i lati che le loro misure.
Prendiamo il lato b come base.
Tracciamo la circonferenza di centro A e raggio a.
Prendiamo a scelta dei punti P₁, P₂, P₃, sulla circonferenza e consideriamo i triangoli AP₁B, AP₂B, AP₃B.
Di ogni triangolo tracciamo le altezze P₁H₁, P₂H₂, P₃H₃.

Domande:
1. quali elementi dei triangoli cambiano e quali no?
2. come varia l’area dei triangoli?
3. quale ti sembra quello che ha l’area maggiore di tutti?

La conclusione è presto trovata: l’area del triangolo è A =½ b ⋅ h e sarà massima quando è massima l’altezza, ovvero quando h=a, cioè per un triangolo rettangolo di cateti a e b.

Passiamo quindi alla ricerca della soluzione ricorrendo al calcolo differenziale e alle proprietà delle funzioni.
Partiamo dalle risposte alla terza domanda.
Nei vari triangoli che abbiamo disegnato, cambiano l’angolo compreso fra i lati assegnati, il terzo lato BC, e l’altezza.
Cerchiamo di ottenere l’espressione dell’area del triangolo in funzione di questi elementi:
Indichiamo con α sia l’angolo, sia la sua misura in radianti.
Indichiamo con x sia il lato BC che la sua misura.
Indichiamo con h sia l’altezza che la sua misura.
Otteniamo:

A( α) = ½ α ab senα  

se scegliamo l’angolo,

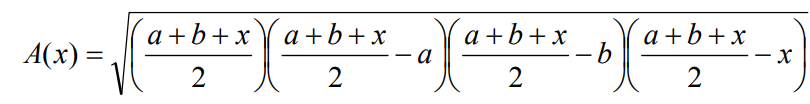
se si sceglie il lato BC e si richiama la formula di Erone,

A =½ b ⋅ h

se si sceglie l’altezza.

Tutte le espressioni esprimono l’area come funzione dell’elemento scelto e sono evidenti le diverse caratteristiche delle funzioni ottenute. La scelta quindi è fondamentale, da essa dipende inevitabilmente la complessità della funzione che si ottiene.
Per risolvere il problema occorre determinare il massimo delle funzioni trovate, tenendo conto che l’elemento della figura (la variabile indipendente delle funzioni) ha delle limitazioni imposte dal problema stesso, e interpretare il risultato geometricamente.
Come esempio focalizziamo l’attenzione su

A( α) = ½ α ab senα  

Vista come funzione, α rappresenta ogni possibile valore reale, ma in realtà, riferendosi alle proprietà dell’elemento scelto, quali valori potrà assumere?
Essendo un angolo di un triangolo potrà assumere tutti i valori compresi nell’intervallo (0,π ) in quanto “la somma degli angoli interni di un triangolo è un angolo piatto”.

E i valori estremi?

Esaminiamo cosa succede. In corrispondenza di tali valori il triangolo degenera in un segmento, l’area sarà nulla. Infatti in corrispondenza di tali valori la funzione determinata assume il valore zero. Comunque sia possiamo prenderli e dire alla fine che α può variare in[0,π ].
In definitiva lo scopo del problema si riassume nel determinare il massimo della funzione

A = ½ α ab senα nell’intervallo [0,π ].

Considerazioni analitiche:

• è una funzione continua sui reali
• l’intervallo è chiuso e limitato
• il teorema di Weierstrass assicura l’esistenza del massimo (e del minimo) su tale intervallo.

Si procede alla ricerca del massimo coi metodi analitici:
a) ricerca dei punti stazionari interni all’intervallo
b) confronto dei valori assunti dalla funzione nei punti stazionari e agli estremi
c) determinazione del valore massimo.

Conclusione:

il triangolo di area massima si ottiene per α = π/2 , in tal caso il triangolo è rettangolo di cateti a e b ed ha area pari a 1/2 *ab

Ovviamente nel caso si consideri la funzione A(x)  le limitazioni per x si ottengono ricordando la disuguaglianza triangolare, e per l’altezza osservando che non può superare il valore del lato a.

IL PROBLEMA DEI RETTANGOLI ISOPERIMETRICI

Il problema isoperimetrico dei rettangoli consiste nel determinare fra tutti i rettangoli di perimetro assegnato, quale abbia l’area massima.

Il problema ha un analogo algebrico.

Sappiamo dire quale sia?

Assegnando il perimetro automaticamente si assegna la somma dei due lati del rettangolo cioè il semiperimetro; l’equivalente algebrico del problema è allora:

dati due numeri reali positivi aventi somma costante, quando è massimo il loro prodotto?

Procediamo alla risoluzione per via analitica.
Sia p il perimetro assegnato di un generico rettangolo.
Indichiamo con x e y sia i lati che le loro misure, nello specifico x rappresenta la base e y l’altezza del rettangolo ABCD.

L’area sarà  A = x ⋅ y . Siamo in presenza di una funzione che dipende da due variabili. Dobbiamo eliminarne una e se ci ricordiamo che il perimetro p = 2(x + y), ecco che

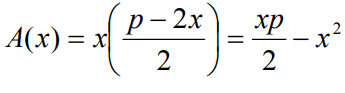
La funzione è facilmente individuabile: si tratta di una parabola passante per l’origine concava con vertice in:

Rappresentiamola

 

Facciamo, prima di giungere alle conclusioni, delle considerazioni su x, (la nostra incognita) in relazione al grafico della parabola.
x rappresenta la misura della base e come tale dovrà essere un numero positivo, inoltre non può superare il valore del semiperimetro.
In corrispondenza dei valori 0 e p/2 il rettangolo degenera infatti in un segmento.

Dobbiamo quindi considerare il grafico della parabola nell’intervallo [0, p/2].

In tale intervallo cade l’ascissa del vertice che è l’unico punto di massimo della parabola.
Il rettangolo di area massima ha la base di misura x = p/4 , y  = p/4 e l’area A = p²/16 .

Si tratta quindi di un quadrato.
Proviamo a questo punto a invertire il problema.
Manteniamo costante l’area e vediamo cosa accade al perimetro.
Traduciamo di nuovo il problema in forma analitica:

x ⋅ y = S , dove S è il valore dell’area assegnata,

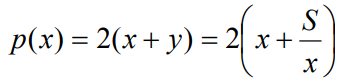
esprime il perimetro.

La funzione che esprime il perimetro ci interessa, tenendo conto sempre che le misure sono positive, per x>0.
Cosa accade per x=0 ?
Ricorrendo ai limiti:

Da un punto di vista geometrico se assegno la misura dell’area, il rettangolo non può essere degenere, quindi ciò spiega il perché la funzione p(x) non è definita per x=0.
Studiando la funzione si perviene alla conclusione che essa ha minimo per x =√ S , in corrispondenza del quale troviamo y = √S , e p = 4√ S .

Il rettangolo di perimetro minimo è il quadrato.
Da sottolineare il fatto che il teorema di Weierstrass non garantisce l’esistenza del massimo e del minimo per x>0 essendo l’intervallo non limitato.
Traiamo come conclusione che: fra i rettangoli di area assegnata il quadrato ha il perimetro minimo.
Analogamente l’equivalente algebrico:

dati due numeri reali positivi aventi prodotto costante, la loro somma è minima quando i due numeri sono uguali.

Concludendo:
• tra i rettangoli di dato perimetro il quadrato ha area massima
• tra i rettangoli di area assegnata il quadrato ha perimetro minimo.

(4003)