
Si determini l’insieme dei punti ove la seguente funzione non è derivabile.

SOLUZIONE
I punti dove la f potrebbe non essere derivabile sono quelli dove
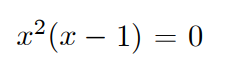
cioè 0 e 1.
Si ha che

per cui in x = 0 la funzione è derivabile. Calcolando la derivata a destra e a sinistra del punto x = 1 si vede che qui la funzione non è derivabile.
ESERCIZIO 2
Si consideri la seguente funzione:

quale delle seguenti proposizioni è vera?
A- f è discontinua in 0 ma è continua e derivabile in tutti gli altri punti
B- f è continua e derivabile in tutti i punti
C- f è continua in tutti i punti e derivabile in tutti i punti escluso 0
D- A,B e C sono false
SOLUZIONE
La proposizione vera è la C.
La funzione è continua in quanto composizione di funzioni continue, si scrive anche come
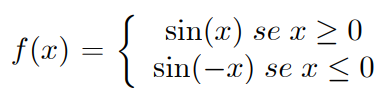
da cui si vede facilmente che è derivabile in tutti i punti escluso x = 0:
Infatti se x < 0 in un intorno piccolo di x

in quell’ intorno.
Analogamente se x > 0 in un intorno piccolo di x:

in quell’ intorno.
Per x = 0 si ha che, per quanto detto prima la derivata destra è 1 e la sinistra è -1.
Quindi la funzione non è derivabile in questo punto.
Teoremi sulle funzioni derivabili
Ricordiamo che a causa del teorema di Lagrange:
Teorema di Lagrange o del valor medio
Ipotesi:
f(x) funzione continua in [a, b] f(x) derivabile in (a, b)Tesi:
esiste almeno un punto x0 appartenente ad (a, b) per cui:
f′(x0) = f(b) − f(a)/(b − a)Significato geometrico del teorema di Lagrange
Se un arco di curva continua in [a,b] è dotato di tangente in tutti i punti dell’intervallo (a,b) esclusi al più gli estremi, allora esiste un punto interno all’arco in cui la tangente è parallela alla corda congiungente gli estremi dell’arco di curva.
Conclusioni:
i) se una funzione è derivabile in (a; b) – x0 e
ii) Se i limiti destro e sinistro esistono e sono diversi la funzione non è derivabile.
iii) se uno dei limiti non esiste la funzione potrebbe anche essere derivabile,
vedi
In questo caso bisogna dimostrare la derivabilità o la non derivabilità in un altro modo.
ESERCIZIO 3
Si determini il punto di minimo della seguente funzione definita sui reali


SOLUZIONE
Si ha che:
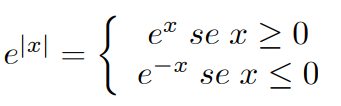
il minimo assoluto e in 0:
Infatti per x < 0 la funzione è decrescente, mentre per x > 0 la funzione è crescente (come si può dimostrare calcolando la derivata).
ESERCIZIO 4
Si consideri la seguente funzione:

quale delle seguenti proposizioni è vera?
A- f è discontinua in 0 ma è continua e derivabile in tutti gli altri punti.
B- f è continua e derivabile in tutti i punti
C- f è continua in tutti i punti e derivabile in tutti i punti escluso 0
D- A,B e C sono false
SOLUZIONE
La risposta giusta è la B.
Infatti si ha che poichè

la funzione è ovviamente derivabile in tutti i punti diversi da zero,
inoltre

da cui si vede che f ‘(0) esiste e vale 0.
Teorema di continuità
Il teorema asserisce che se f(x) è derivabile in x0 allora f(x) è anche continua in x0.
Notiamo che l’inverso non è sempre vero: ad esempio, la funzione f(x) = | x | è continua su tutto il dominio, ma non è derivabile nel punto x = 0, perché la derivata destra non coincide con la derivata sinistra. La continuità di una funzione è quindi condizione necessaria, ma non sufficiente, per determinarne la derivabilità.
ESERCIZIO 5
Si determini il punto di minimo della seguente funzione definita sui reali:

SOLUZIONE
Il minimo cercato non esiste, in quanto per x → -∞ la funzione assume valori piccoli quanto si vuole sen(x) è limitato, x decresce a -∞.
ESERCIZIO 6
Si determini il punto di minimo della seguente funzione definita sui reali:

SOLUZIONE
Si noti che esistono punti dove

In questi punti anche f(x) = 0. Poichè la funzione data assume solo valori positivi si ha che questo è il valore minimo.
ESERCIZIO 7
Sia C1 [0; 1] l’ insieme delle funzioni aventi derivata continua in [0; 1];
sia X l’ insieme definito da

A- X contiene solo la funzione f(x) = 0
B- X contiene un numero finito di elementi
C- X contiene un numero infinito di elementi
D- nessuna delle risposte precedenti
SOLUZIONE
L’insieme considerato contiene un numero infinito di elementi.
Per dimostrarlo, ad esempio si può cominciare con il cercare una qualsiasi funzione non nulla che appartiene a X:
Ad esempio si consideri la funzione

Data una tale funzione anche Cf(x) per ogni C reale appartiene a X.
Quindi ce ne sono infinite.
(1540)


