La formula di Taylor

La formula di Taylor è una formula che ci fornisce approssimazioni sempre migliori di una funzione data f(x) in un intorno di un suo punto x₀ e grazie alla quale si possono ricavare importanti informazioni sul comportamento della funzione vicino a x₀ (in particolare se è crescente, decrescente, convessa, concava, se ha massimi o minimi).
Prima di dare la formula generale, giusto per avere un’idea di che tipo di approssimazione si tratti e cosa significhi ”approssimazioni sempre migliori”, ecco come si presenta ad esempio la formula di Taylor per la funzione f(x) =e^x , approssimata in un intorno di x₀ = 0:

Il significato della prima espressione è la seguente: in un intorno di x₀ = 0, la funzione e^x si può approssimare mediante il polinomio di primo grado 1+x, con un errore o(x) che ha la proprietà che per x → 0 non solo o(x) tende a zero (e quindi più ci avviciniamo al punto più diventa piccolo come errore) ma ci va più velocemente di x, ovvero

La seconda espressione significa invece che la funzione e^x si può approssimare ancora meglio mediante il polinomio di secondo grado

con un errore o(x²) che stavolta ha la proprietà che per x → 0 tende a zero più velocemente di x²  ovvero

quindi anche più velocemente dell’o(x) dell’approssimazione precedente, e in questo senso rappresenta un’approssimazione migliore.

Le due espressioni scritte sopra si dicono sviluppo di Taylor arrestato rispettivamente al primo e al secondo  ordine. In generale, potremmo
andare avanti e considerare lo sviluppo arrestato all’n-esimo ordine, con n qualunque, dove a patto di usare un polinomio di grado n sempre più alto, avremmo un’approssimazione sempre migliore commettendo un errore di approssimazione sempre più piccolo, o per meglio dire un errore che va a zero sempre più velocemente per x che tende al punto x₀ = 0 in cui stiamo approssimando la funzione.
A consentire quest’approssimazione sempre migliore è, come vedremo ora dando la formula generale, il fatto che la funzione e^x è derivabile quante volte vogliamo.

In generale, data una funzione f(x) e un punto x₀, si può costruire il suo sviluppo di Taylor arrestato all’n-esimo ordine, con n uguale a un certo numero naturale 1, 2, 3, 4 etc. sotto l’ipotesi che f sia derivabile n volte in x₀, cioè che esistano e siano finite le derivate f ‘(x₀), f ”(x₀) etc. fino alla derivata n-esima f⁽ⁿ⁾(x₀).

In tal caso, la formula è la seguente:

 

dove si ricordi che il fattoriale n! di un numero naturale n è uguale al prodotto di n per tutti i naturali precedenti (0 escluso), ovvero

2! = 2 · 1 = 2
3! = 3 · 2 · 1 = 6
4! = 4 · 3 · 2 · 1 = 24

etc. e dove o((x − x0)ⁿ) rappresenta l’errore di approssimazione, che ha la proprietà di andare a zero per x → x₀ più velocemente di (x − x₀)ⁿ. Si dice anche che o((x − x₀)ⁿ) è un ”o piccolo di (x − x₀)ⁿ.

Osservazione

Si noti che lo sviluppo di Taylor del prim’ordine di una funzione f in x₀ sta approssimando f con la funzione polinomiale di primo grado:

il cui grafico rappresenta esattamente la retta tangente al grafico di f in x₀. Da un punto di vista geometrico, possiamo quindi affermare che l’approssimazione al prim’ordine non fa altro che approssimare il grafico di f con il grafico della sua retta tangente nel punto considerato (mentre con lo sviluppo arrestato al second’ordine avremmo che stiamo approssimando f con un polinomio di secondo grado in x e quindi il grafico di f con quello di una parabola).

Ora vedremo le importantissime applicazioni della formula di Taylor cui accennavamo all’inizio, ovvero la determinazione di informazioni sul comportamento della funzione vicino al punto x₀ di approssimazione e in particolare informazioni sulla sua crescenza, decrescenza,
convessità etc.

Criteri di convessità/concavità

Iniziamo a vedere in che modo la formula di Taylor ci dà informazioni sulla convessità/concavità di una funzione. La prima affermazione che vorremmo mostrare è la seguente:

Se f ”(x₀) > 0 allora in un intorno di x₀ la funzione è convessa; se f ”(x₀) < 0 allora in un intorno di x₀ la funzione è concava.

Per verificare l’affermazione, useremo il fatto che una funzione (derivabile) è convessa in un intorno di un punto esattamente quando sta al di sopra della retta tangente in quel punto, mentre è concava quando sta invece al di sotto della retta tangente.

Avevamo definito una funzione convessa o concava quando il suo grafico compreso tra due punti sta rispettivamente sotto o sopra il segmento congiungente i due punti, ma si può dimostrare che questa condizione è equivalente a quella appena data sulla retta tangente.

Ricordiamo che l’equazione della retta tangente in un x₀ al grafico di f è

Quindi, per valutare se il grafico di y = f(x) sta sopra o sta al di sotto del grafico della retta (e capire quindi se f è convessa o concava) dobbiamo semplicemente controllare se è

ovvero equivalentemente valutare se è positiva o negativa la differenza

A questo scopo, usiamo lo sviluppo di Taylor di f in x₀ arrestato al second’ordine, portando a primo membro i primi due addendi del secondo membro e dividendo entrambi i membri di questa uguaglianza per (x − x₀)² 

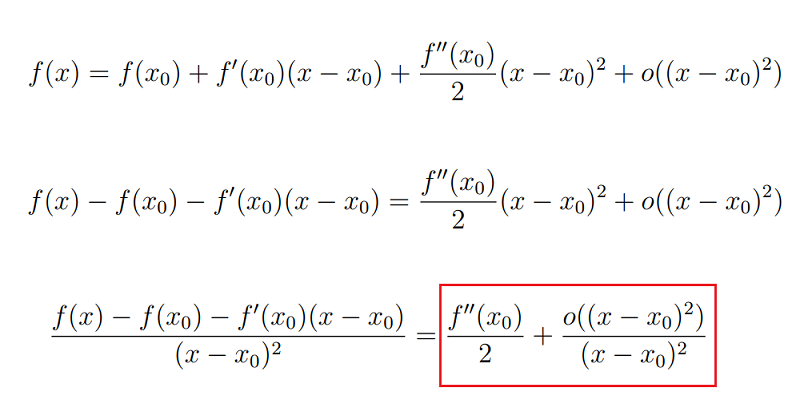
Ora, se facciamo tendere x a x₀, come sappiamo l’ultimo addendo tende a zero, quindi il secondo membro dell’uguaglianza tende a

che non dipende da x, quindi mandando al limite rimane così com’è; cioè riassumendo, posso concludere che per x che tende a x₀ ho

Ora, se f ”(x₀) > 0 allora

sta tendendo a una quantità positiva. Questo vuol dire che se mi metto abbastanza vicino a x₀ devo avere per forza

e quindi (essendo il denominatore sempre positivo perchè è un quadrato) ho il numeratore
f(x)−f(x₀)−f ‘(x₀)(x−x₀₎ > 0,

cioè

f(x) > f(x₀) + f ‘(x₀)(x−x₀):

questo significa che in un intorno di x₀ il grafico di f sta sopra la retta tangente.

Analogamente, se f ”(x₀) < 0: in un intorno di x₀ il grafico di f sta sotto la retta tangente.

Cosa possiamo dire riguardo alla convessità e concavità della funzione se invece f ”(x₀) = 0?

In tal caso, lo sviluppo di Taylor arrestato al secondo ordine sarebbe:

f(x) = f(x₀) + f ‘(x₀)(x − x₀) + o((x − x₀)²)

ovvero, portando a primo membro i primi due addendi,

f(x)- f(x₀) – f ‘(x₀)(x − x₀) = o((x − x₀)²)

 

e non riusciremmo a ottenere nessuna informazione sul segno della differenza f(x)- f(x₀) – f ‘(x₀)(x − x₀) (che si dice se il grafico di f sta sopra o sotto la retta tangente), perchè l’unica quantità che rimane a secondo membro è o((x − x₀)²) del quale sappiamo solo che tende a zero ma senza sapere nulla del segno che ha avvicinandosi a zero.

Per ovviare a questo problema, miglioriamo la nostra approssimazione considerando allora lo sviluppo arrestato al terz’ordine

dove non abbiamo scritto l’addendo relativo alla derivata seconda, perchè siamo nell’ipotesi che essa sia nulla.

Proviamo a replicare lo stesso ragionamento fatto nel caso precedente:
portiamo a primo membro i primi due addendi e dividiamo ora entrambi i membri per (x − x₀)³:

che è l’analogo del caso precedente caso precedente.
Arrivati a questo punto, potremmo essere tentati di concludere  che quando f ”'(x₀) è positiva allora f(x) − f(x₀) − f ‘(x₀)(x − x₀) è positivo, e quando f ”'(x₀) è negativo allora f(x) − f(x₀) − f ‘(x₀)(x − x₀) è negativo: tuttavia, questo non è corretto!

Mentre nel caso precedente il denominatore del rapporto era (x−x₀)² e non aveva nessun ruolo nel determinare il segno, in quanto sempre
positivo essendo un quadrato, stavolta ) il denominatore `e il cubo(x − x₀)³, che invece non è sempre positivo, ma è positivo per x − x₀ > 0,
cioè quando x > x₀ (diremo ”a destra di x₀”) e negativo per x − x₀ < 0, cioè quando x < x₀ (diremo ”a sinistra di x₀”).

Questo complica leggermente la discussione, vediamo i dettagli:

(i) Sia f ”'(x₀) > 0.

Allora, a destra di x₀ (dove il cubo a denominatore è positivo) il numeratore deve essere
f(x) − f(x₀) − f ‘(x₀)(x − x₀) > 0, mentre a sinistra di x₀ (dove il cubo a denominatore è negativo) il numeratore deve essere

f(x) − f(x₀) − f ‘(x₀)(x − x₀) < 0 (affinchè il rapporto rimanga positivo).

Quindi, riassumendo,

per x > x₀ devo avere f(x) > f(x₀) − f ‘(x₀)(x − x₀) mentre
per x < x₀ devo avere f(x) < f(x₀) − f ‘(x₀)(x − x₀).

Quindi il grafico della funzione sta sopra la retta tangente a destra di x₀ e sotto la retta tangente a sinistra di x₀ ed attraversa la retta tangente nel passare da sinistra a destra di x₀, passando da concava a convessa: un tale punto si dice di flesso. 

(ii) Sia f ”'(x₀) > 0.

Simmetricamente

il grafico di f stavolta è sotto quello della retta tangente a destra di x sopra la retta tangente a sinistra di x₀: il grafico di f attraversa la retta tangente nel passare da sinistra a destra di x₀, stavolta passando da convessa a concava, e abbiamo quindi ancora un cosiddetto punto di flesso. 

A questo punto sorge spontanea la domanda: e se fosse anche f ”'(x₀) = 0? E se fossero nulle anche altre derivate superiori alla terza?
I due casi che abbiamo studiato in precedenza ci suggeriscono che il comportamento della funzione dipende non solo da qual è il segno della prima derivata non nulla in x₀ ma ci suggeriscono anche il fatto che la conclusione cambia a seconda che questa derivata sia di ordine pari o dispari.

Generalizzando, otteniamo il criterio più generale possibile:

 

Sia data una funzione f che sia derivabile almeno n volte in x₀ e tale che la sua prima derivata non nulla in x₀ è f⁽ⁿ⁾(x₀) (con n ≥ 2). Allora
(i) Se n è pari, la funzione è convessa se f⁽ⁿ⁾(x₀) > 0 e concava se  f⁽ⁿ⁾(x₀) < 0
(ii) Se n è dispari, la funzione ha un flesso in x₀, e in particolare passa da concava a convessa se f⁽ⁿ⁾(x₀)> 0 e da convessa a concava se  f⁽ⁿ⁾(x₀) < 0.

 

(1270)