
Indice
Funzioni reali: limiti e continuità
Esercizio 1
Si consideri la funzione f il cui grafico è rappresentato nella figura in basso:

(i) Si determinino (se hanno senso e se esistono) i seguenti limiti
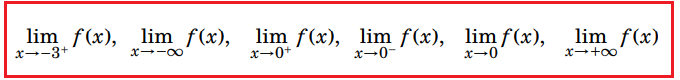
(ii) Si determinino gli eventuali punti del dominio in cui f è discontinua.
(iii) Ha senso dire che f è continua in x = +∞? Eventualmente precisarne il senso.
(iv) Ha senso dire che f è continua in x = −3? Eventualmente precisarne il senso.
(v) Detto Df il dominio di f , stabilire se il teorema di Weierstrass è applicabile a f nell’intervallo [−1,1], cioè a f |[−1,1]∩Df.
(vi) Stabilire se f ammette massimo e minimo su [−1,1]∩Df.
(vii) Stabilire se il teorema degli zeri è applicabile a f nell’intervallo [−1,1].
(viii) Stabilire se esiste c ∈ (−1,1) tale che f (c) = 0.
(ix) Stabilire se il teorema degli zeri è applicabile a f nell’intervallo [−3,−1].
(x) Stabilire se esiste c ∈ (−3,−1) tale che f (c) = 0.
Soluzione
(i) Si ha:

(ii) Nessuno.
Definizione di Continuità.
Sia f : A → R e sia x0 ∈ A. f si dice
(i) continua a destra in x0 se f (x0) = limx→x0+ f (x).
(ii) continua a sinistra in x0 se f (x0) = limx→x0– f (x).
(iii) continua in x0 se è sia continua a destra, sia continua a sinistra in x0, equivalentemente se f (x0) = limx→x0f(x).
Inoltre, se I ⊆ A è un intervallo, si dice che f è continua in I se essa è continua in ogni x0 ∈ I. Nel caso in cui x0 sia un estremo dell’intervallo I tale continuità va intesa come
• continuità a destra, nel caso in cui x0 sia l’estremo sinistro dell’intervallo;
• continuità a sinistra, nel caso in cui x0 sia l’estremo destro dell’intervallo.
(iii) Non ha senso: +∞ ∉ R.
(iv) Si, nel senso di continua a destra,
(v) Non è applicabile. La funzione non è definita su tutto [−1,1] (infatti 0 ∉ Df).
Teorema di Weierstrass
Sia f : [a,b] → R continua (su [a,b]). Allora f ha massimo e minimo su [a,b].
Teoremi sulle funzioni derivabili
Esercizio 2
Si consideri la funzione f il cui grafico è rappresentato nella figura in basso:

(i) Si determinino (se hanno senso e se esistono) i seguenti limiti
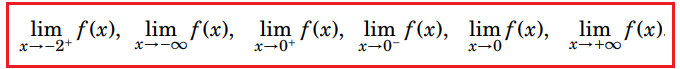
(ii) Si determinino gli eventuali punti del dominio in cui f è discontinua.
(iii) Ha senso dire che f è continua in x = −2? Eventualmente precisarne il senso.
(iv) Ha senso dire che f è continua in x = 2? Eventualmente precisarne il senso.
(v) Detto Df il dominio di f , stabilire se il Teorema di Weierstrass è applicabile nell’intervallo [−1,1], cioè a f |[−1,1]∩Df.
(vi) Stabilire se f ammette massimo e minimo nell’intervallo [−1,1].
(vii) Stabilire se il teorema dei valori intermedi è applicabile a f nell’intervallo [−2,−1].
(viii) Stabilire se esiste c ∈ [−2,−1] tale che f (c) = 0.
Soluzione
(i) Si ha:

(ii) In x = 0.
(iii) Si, nel senso di continua a destra.
(iv) Si, nel senso di continua a sinistra.
(v) Non è applicabile. La funzione non è continua in x = 0.
(vi) Ammette minimo, di valore 1, in x = ±1 ∨ x = 0. Non ammette massimo.
(vii) Si, tutte le ipotesi sono soddisfatte. Se ne deduce che f assume nell’intervallo [−2,1] tutti i valori compresi tra f (−2) = 0 e f (−1) = 1.
Teorema della permanenza del segno
Sia I ⊆ R un intervallo e sia f : I → R continua su I. Si assuma che in un dato punto c ∈ I risulti f (c) > 0 (risp., f (c) < 0). Allora esiste
δ > 0 tale che f (x) > 0 (risp., f (x) < 0) per ogni x ∈ I ∩(c −δ, c +δ).Corollario Teorema dei valori intermedi – I forma.
Sia f : [a,b] → R continua (su [a,b]).
Allora f assume tutti i valori compresi tra min{f (a), f (b)} e max{f (a), f (b)}.Corollario Teorema dei valori intermedi – II forma
Sia f : [a,b] → R continua (su [a,b]). Allora f assume tutti i valori compresi tra min[a,b]f e max[a,b]f .
(viii) Si, f (−2) = 0.
Esercizio 3
Si dica per quali valori dei parametri a,b ∈ R la seguente funzione è continua su R.

Soluzione
La funzione f è continua per ogni valore di a,b ∈ R separatamente negli intervalli in (0,+∞), (−1,0] e (−∞,−1), in quanto essa è definita, su ciascuno di questi pezzi del dominio, attraverso operazioni algebriche che non prevedono divisioni per 0 e composizione di funzioni elementari.
Resta da imporre la continuità a destra in x = 0 e in x = −1 che corrisponde al sistema:

Da cui si deduce che f è continua se e solo se a = 1− e ∧ b = e.
Esercizio 4
Si dica per quali valori dei parametri a < 1 e b ∈ R la seguente funzione è continua su R.

Soluzione
La funzione f è continua per ogni valore di a < 1 e b ∈ R separatamente negli intervalli (−a,+∞), in (−1,−a] e in (−∞,−1], in quanto essa è definita, su ciascuno di questi pezzi del dominio, attraverso operazioni algebriche che non prevedono divisioni per 0 e composizione di funzioni elementari.
Resta da imporre la continuità a destra in x = −a e in x = −1 che corrisponde al sistema:

L’equazione in a non ha ha soluzioni, per cui la funzione data non è mai continua su R qualunque sia il valore dei parametri a < 1 e b ∈ R.
Esercizio 5
(i) Si esibisca una funzione f : (0,1] → R continua su (0,1], che non ammette massimo su (0,1].
(ii) Si esibisca una funzione f : (0,1] → R continua su (0,1], che non ammette minimo su (0,1].
(iii) Si esibisca una funzione f : [0,+∞) → R continua su [0,+∞), che non ammette né massimo né minimo su [0,+∞).
(iv) Si esibisca una funzione f : (0,1] → R continua (0,1], che non che non ammette né massimo né minimo su (0,1].
Soluzione
(i) f : (0,1] → R, f (x) = −x.
(ii) f : (0,1] → R, f (x) = x.
(iii) f : [0,+∞) → R, f (x) = xsin x.
(iv)

(1175)
