
Indice
Teoremi sulle funzioni derivabili
Teorema di Rolle
Sia f una funzione definita in un intervallo chiuso [a, b] e avente le seguenti proprietà:
1. f è continua in [a, b] (compresi gli estremi!);
2. f è derivabile almeno in ]a, b[ (potrebbe non essere derivabile negli estremi, per esempio potrebbe avere derivata infinita negli estremi);
3. f (a) = f (b) (le “quote” iniziale e finale del grafico sono identiche).
Allora esiste almeno un punto c interno ad [a, b] dove la derivata prima del la funzione si annulla.
Le figure che seguono danno una giustificazione grafica di questo risultato, se si tiene conto che avere derivata nulla significa avere tangente orizzontale. Il punto (o i punti di cui parla il teorema si possono chiamare “ punti di Rolle” ).

Cosa significa ” condizione sufficiente”
Approfittiamo di questo teorema per fare delle osservazioni su che cosa significhi condizione sufficiente. Le tre condizioni presenti nell’enunciato di questo teorema sono delle condizioni sufficienti per la validità dello stesso. Infatti se anche una o più di queste condizioni manca, non si può concludere con la tesi, come dimostrano i tre grafici che seguono:
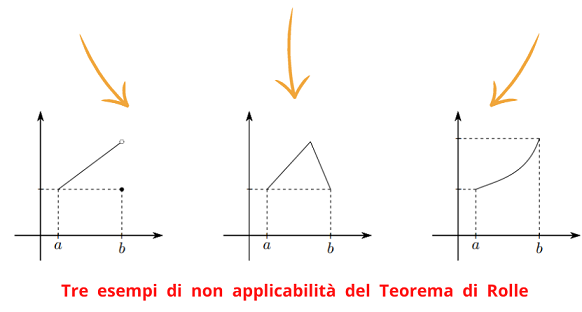
- nel primo manca solo l’ipotesi di continuità in tutto [a,b],
- nel secondo manca solo l’ipotesi di derivabilità all’interno di [a, b],
- nel terzo manca solo l’ipotesi che le quote agli estremi siano uguali.
In tutti e tre i casi non esiste alcun punto di Rolle.
Teorema di Rolle tre esempi di inapplicabilità
Tutto questo non significa affatto che se mancano una o più delle tre condizioni presenti nell’enunciato del teorema non esiste alcun punto di Rolle, come mostra il seguente grafico, in cui mancano addirittura tutte e tre le condizioni, ma dove esistono addirittura due punti in cui il grafico ha tangente orizzontale.
Un esempio in cui esistono punti di Rolle, nonostante le ipotesi non siano verificate

Il motivo di questo comportamento è da ricercarsi nel fatto che le condizioni per la validità del Teorema di Rolle non sono necessarie: anche se mancano, la tesi può essere ugualmente vera.
Esempio
Se una funzione soddisfa le ipotesi del teorema, almeno un punto di Rolle esiste sicuramente.
Per trovarlo analiticamente basterà risolvere l’equazione, nell’incognita c, f ‘(c) = 0.
Consideriamo la funzione, avente dominio l’intervallo [0, 1],
![]()
Essa soddisfa chiaramente le ipotesi del teorema di Rolle, per cui deve esistere almeno un punto c, interno al dominio, dove f ‘ (c) = 0. Per trovarlo basterà risolvere l’equazione:

Solo il punto c = 2/3 va bene, perchè l’altro è situato proprio sulla frontiera del dominio.
Esempio
Consideriamo, nell’intervallo [-1; 1], la funzione f(x) = x4 – 2x2.
f(x) è continua e derivabile per ogni x∈ R, e ha derivata f ‘(x )= – 4x3 -4x.
Inoltre f(-1) = – 1 = f(1).
Quindi sono verificate le ipotesi del teorema di Rolle.
In questo caso, esistono tre punti in [-1; 1] per i quali la derivata si annulla,
infatti:

In particolare, x2 ∈ ]-1; 1[ e quindi il teorema è verificato.
Esempio
Consideriamo la funzione:

nell’intervallo [ 0;2].
Il teorema di Rolle è applicabile?
Verifichiamo le ipotesi del teorema
1) La funzione deve essere continua nell’intervallo chiuso [0,2], cioè estremi compresi; per fare ciò si calcola il dominio della funzione. Essendo una funzione fratta si pone il denominatore diverso da zero.

2) La funzione deve essere derivabile nell’intervallo aperto, cioè esclusi gli estremi, (0,2); quindi calcolo la derivata prima della funzione, e poi ne calcolo il suo dominio.
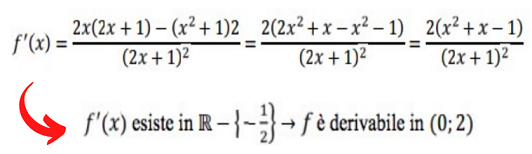
3) f(a) = f(b) → f(0) = f(2)
Sostituisco 0 e 2 nella funzione al posto della x, e vedo se i risultati sono uguali.

Tutte e tre le ipotesi del teorema di Rolle sono verificate → il teorema è applicabile.
Ora troviamo c tale per cui f ‘(c) = 0.

(703)
