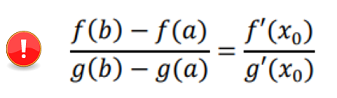
TEOREMA DI CAUCHY

Se f(x) e g(x) sono due funzioni continue nell’intervallo chiuso [a,b] e derivabili internamente ad esso, e se la derivata g'(x) non si annulla mai, esiste almeno un punto x₀ , interno ad [a,b], in cui risulta:

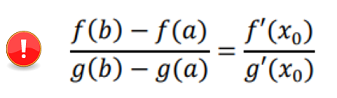
APPLICAZIONE TEOREMA DI CAUCHY

Esercizio 1

Applicare il teorema di Cauchy alle funzioni

f(x) = 3x² -1 
g(x) = 6x

nell’intervallo [0,1]

Soluzione

Calcoliamo la derivata prima di entrambe le funzioni:

f ‘(x) = 6x;   g'(x) = 4

Calcoliamo il dominio delle funzioni f(x) e g(x):

continue in R e dunque in [0,1]

Calcoliamo il dominio delle derivate f ‘(x) e g'(x):

derivabili in R e dunque in (0,1)

Il teorema è applicabile!

Quindi esiste un punto c che appartiene all’intervallo (0,1) tale che:

c = ½ è interno all’intervallo (0,1), quindi è accettabile.

Esercizio 2

Verificare se le funzioni 𝑓 e 𝑔 soddisfano , nell’intervallo  indicato, le ipotesi del teorema di Cauchy e, in caso affermativo, determinare i punti che verificano il teorema.

𝑓(𝑥) = 𝑥² − 2𝑥

𝑔(𝑥) = 𝑥² + 3𝑥+4

𝐼 = [0; 1]

Soluzione

Le funzioni date sono continue e derivabili in ℝ, quindi in 𝐼 = [0; 1] , inoltre

𝑔′(𝑥) = 2𝑥 + 3 ≠ 0 ∀𝑥 ∈ 𝐼

Ne segue che sono verificate le ipotesi del teorema e risulta:

Esercizio 3

Verificare se le funzioni 𝑓 e 𝑔 soddisfano , nell’intervallo  indicato, le ipotesi del teorema di Cauchy e, in caso affermativo, determinare i punti che verificano il teorema.

f(𝑥) = 2𝑥 − 𝑥³
𝑔(𝑥) = 𝑥² − 4𝑥

𝐼 = [−1; 1]

Soluzione

Le funzioni sono continue e derivabili in ℝ , quindi lo sono in I = [−1; 1].

Si ha :

𝑓′(𝑥) = 2 − 3𝑥²  , 𝑔′(𝑥) = 2𝑥 − 4   ≠ 0 ∀ 𝑥 ∈ I.

Sono quindi verificate le ipotesi del Teorema di Cauchy .

Si ha:

Le soluzioni sono entrambi  punti di Cauchy perché  interni all’intervallo I.

Esercizio 4

Verificare se le funzioni 𝑓 e 𝑔 soddisfano , nell’intervallo  indicato, le ipotesi del teorema di Cauchy e, in caso affermativo, determinare i punti che verificano il teorema.

𝑓(𝑥) = 𝑥² + 4

𝑔(𝑥) = 𝑒^𝑥
𝐼 = [0; 1]

Soluzione

Le funzioni date sono continue e derivabili in ℝ, quindi in 𝐼 = [0; 1] , inoltre

𝑔′(𝑥) = 𝑒^𝑥 ≠ 0 ∀𝑥 ∈ ℝ

Ne segue che sono verificate le ipotesi del teorema e risulta:

La radice si può accertare applicando il teorema di esistenza degli zeri alla funzione continua

ℎ(𝑥) = 𝑒^𝑥 − 2(𝑒 − 1)x

relativamente all’intervallo 𝐼 = [0; 1].

Poiché ℎ(0) = 1 > 0 e ℎ(1) = −𝑒 + 2 < 0 , si deduce che esiste in (0; 1) il punto che verifica il teorema.

(3346)