Cos’è un intervallo di confidenza

Ci sono due approcci fondamentali di stima: le stime puntuali e le stime per intervalli.

• La stima puntuale è lo specifico valore assunto da una statistica, calcolata in corrispondenza dei dati campionari e che viene utilizzata per stimare il vero valore non noto di un parametro di una popolazione
• Uno stimatore per intervallo è un intervallo costruito attorno allo stimatore puntuale, in modo tale che sia nota e fissata la probabilità che il parametro appartenga all’intervallo stesso. Tale probabilità è detta livello di confidenza ed è in generale indicato con (1−α)% dove α è la probabilità che il parametro si trovi al di fuori dell’intervallo di confidenza.
•  Quindi la confidenza è il grado di fiducia che l’intervallo possa contenere effettivamente il parametro di interesse.

Intervallo di confidenza per la media (σ noto)

Varianza nota

Si tratta di un caso abbastanza raro nelle applicazioni, ma in certe circostanze è possibile che indagini precedenti a quella effettuata rendano possibile una conoscenza esatta della varianza σ² .

ESEMPIO

Si consideri un processo industriale di riempimento di scatole di cereali e sia assuma che il peso X delle scatole sia

X~ N(µ;15²).

Dato un campione casuale di n=25 scatole con peso medio 362.3 grammi si vuole costruire un intervallo di confidenza al 95% per µ.
Per la proprietà della distribuzione normale e della media campionaria risulta che

quindi un intervallo di confidenza all’(1−α)% per µ è dato da

Nel caso specifico si ottiene 356.42 ≤ µ ≤ 368.18.

Ipotizziamo che µ sia uguale a 368. Per comprendere a fondo il significato della stima per intervallo e le sue proprietà è utile fare riferimento all’ipotetico insieme di tutti i possibili campioni di ampiezza n che è possibile ottenere.

Osserviamo che per alcuni campioni la stima per intervalli di µ è corretta, mentre per altri non lo è.

Nella pratica estraiamo un solo campione e siccome non conosciamo la media della popolazione non possiamo stabilire se le conclusioni a cui perveniamo sono corrette o meno.
Tuttavia possiamo affermare di avere una fiducia all’(1−α)% che la media appartenga all’intervallo stimato.
Quindi, l’intervallo di confidenza all’(1−α)% della media con σ noto si ottiene utilizzando l’equazione:

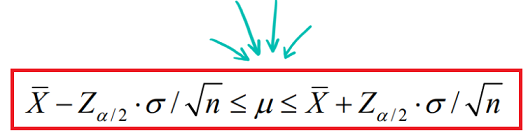
dove Z_α/2 è il valore a cui corrisponde un’area cumulata pari a (1−α/2) della distribuzione normale standard.

Il valore Zα/2 di Z che viene scelto per costruire un intervallo di confidenza è chiamato valore critico. A ciascun livello di confidenza (1−α) corrisponde un diverso valore critico.

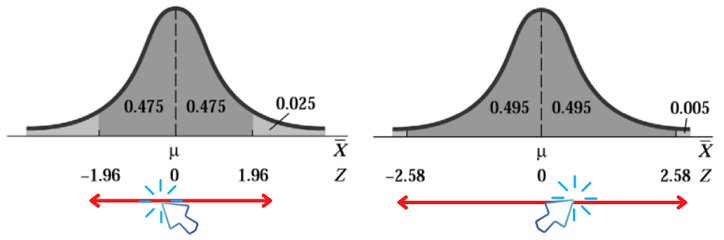
Un livello di confidenza maggiore si ottiene quindi a prezzo di un ampliamento dell’intervallo di confidenza ottenuto: esiste un trade-off tra utilità pratica dell’intervallo e livello di confidenza.

Esercizio 1

Un laboratorio analizza una certa quantità di un prodotto farmaceutico per determinare la concentrazione di principio attivo in esso presente. Tali analisi non sono perfettamente precise; se vengono ripetute per altre quantità estratte dal medesimo prodotto i risultati seguono una distribuzione normale con media µ, concentrazione del principio attivo nel prodotto incognita e deviazione standard, caratteristica della procedura analitica usata, nota e pari a

Il laboratorio analizza 4 quantità estratte dal prodotto ottenendo i seguenti risultati:  

la casa farmaceutica è interessata ad un intervallo di confidenza per la concentrazione di principio attivo presente nel prodotto al 90%, determinarlo. Calcolare, inoltre, l’intervallo di confidenza per la concentrazione di principio attivo presente nel prodotto al 99%.

Soluzione

Indichiamo con X la variabile casuale in esame. Per ipotesi si ha:

Per determinare l’intervallo di confidenza per la media di una popolazione normale con varianza nota, si ricorre alla variabile

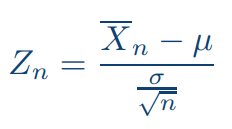
che è distribuita come una normale di media 0 e varianza 1.

Intervallo di confidenza: media con varianza nota

Fissato il livello di confidenza 1 − α e indicato con z_α/2 il percentile tale che

 

dall’intervallo di probabilità per la variabile casuale con distribuzione normale standardizzata si ha:

Effettuando alcuni passaggi algebrici e sostituendo i valori campionari osservati si ottiene

Essendo:

e

L’intervallo di confidenza per il parametro µ risulta pari a

Se il livello di confidenza è al 99%, l’intervallo di confidenza per il parametro µ risulta:

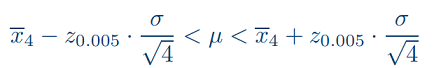
Esercizio 2

Un segnale radio viene emesso con frequenza distribuita normalmente e con valore atteso µ e deviazione standard 30 kHz. Supponendo di osservare la seguente serie di frequenze in kHz:

determinare una stima di µ e la probabilità che la frequenza stia nell’intervallo [590 kHz, 610 kHz]. Determinare poi un intervallo di confidenza per µ al 95 per cento.

Soluzione

Sia X la v.c. che denota la frequenza del segnale radio emesso, si ha X˜N (µ, 900). Lo stimatore per µ è X₁₅ , la stima di µ richiesta è

 

Determiniamo ora la P [590 ≤ X ≤ 610]:

Per determinare l’intervallo di confidenza per la media, essendo la distribuzione normale di varianza nota, si ricorre alla variabile

 

L’intervallo di confidenza bilaterale al livello 0, 95 = 1 − α per µ è

Consultando le tavole della normale, troviamo che z_0.025

 

quindi sostituendo con

Supponiamo invece di voler ricavare per µ un intervallo di confidenza unilaterale al 95 per cento:

Intervallo destro

Posto:

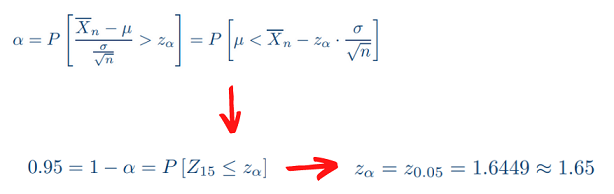
Sostituendo

Intervallo sinistro

(320)